An implementation of funnel plots for indirectly standardised ratios, as described by Spiegelhalter (2005) <https://doi.org/10.1002/sim.1970/>. There are several parameters for the input, with the assumption that you will want smooth, overdispersed, funnel control limits. Limits may be inflated for overdispersion based on the methods of DerSimonian & Laird (1986), buy calculating a between unit standard deviation (\(\tau\)) and constructing an additive random effects models, originally used for meta-analyses of clinical trials data.
funnel_plot(
.data,
numerator,
denominator,
group,
data_type = "SR",
limit = 99,
label = "outlier",
highlight = NA,
draw_unadjusted = FALSE,
draw_adjusted = TRUE,
sr_method = "SHMI",
trim_by = 0.1,
title = "Untitled Funnel Plot",
multiplier = 1,
x_label = "Expected",
y_label,
x_range = "auto",
y_range = "auto",
plot_cols = c("#FF7F0EFF", "#FF7F0EFF", "#1F77B4FF", "#1F77B4FF", "#9467BDFF",
"#9467BDFF", "#2CA02CFF", "#2CA02CFF"),
theme = funnel_clean(),
label_outliers,
Poisson_limits,
OD_adjust,
xrange,
yrange,
SHMI_rounding = TRUE,
max.overlaps = 10
)Arguments
- .data
A data frame containing a numerator, denominator and grouping field.
- numerator
A vector of the numerator (observed events/counts) values. Used as numerator of the Y-axis
- denominator
A vector of denominator (predicted/population etc.) Used as denominator of the Y-axis and the scale of the x-axis
- group
A vector of group names as character or factor. Used to aggregate and group points on plots
- data_type
A string identifying the type of data used for in the plot, the adjustment used and the reference point. One of: "SR" for indirectly standardised ratios, such SHMI, "PR" for proportions, or "RC" for ratios of counts. Default is "SR".
- limit
Plot limits, accepted values are: 95 or 99, corresponding to 95% or 99.8% quantiles of the distribution. Default=99,and applies to OD limits if both OD and Poisson are used.
- label
Whether to label outliers, highlighted groups, both or none. Default is "outlier", by accepted values are:
"outlier"- Labels upper and lower outliers, determined in relation to the `limit` argument."outlier_lower"- Labels just and lower outliers, determined in relation to the `limit` argument."outlier_upper"- Labels just upper, determined in relation to the `limit` argument."highlight"- Labels the value(s) given in the `highlight`argument."both"- Labels both the highlighted values(s), upper and lower outliers, determined in relation to the `limit` argument."both_lower"- Labels both the highlighted values(s) and lower outliers, determined in relation to the `limit` argument."both_upper"- Labels both the highlighted values(s) and upper outliers, determined in relation to the `limit` argument.NA- No labels applied
- highlight
Single or vector of points to highlight, with a different colour and point style. Should correspond to values specified to `group`. Default is NA, for no highlighting.
- draw_unadjusted
Draw control limits without overdispersion adjustment. (default=FALSE)
- draw_adjusted
Draw overdispersed limits using hierarchical model, assuming at group level, as described in Spiegelhalter (2012). It calculates a second variance component ' for the 'between' standard deviation (\(\tau\)), that is added to the 'within' standard deviation (sigma) (default=TRUE)
- sr_method
Method for adjustment when using indirectly standardised ratios (type="SR") Either "CQC" or "SHMI" (default). There are a few methods for standardisation. "CQC"/Spiegelhalter uses a square-root transformation and Winsorises (rescales the outer most values to a particular percentile). SHMI, instead, uses log-transformation and doesn't Winsorise, but truncates the distribution before assessing overdisperison . Both methods then calculate a dispersion ratio (\(\phi\)) on this altered dataset. This ratio is then used to scale the full dataset, and the plot is drawn for the full dataset.
- trim_by
Proportion of the distribution for winsorisation/truncation. Default is 10 % (0.1). Note, this is applied in a two-sided fashion, e.g. 10% refers to 10% at each end of the distribution (20% winsorised/truncated)
- title
Plot title
- multiplier
Scale relative risk and funnel by this factor. Default to 1, but 100 sometime used, e.g. in some hospital mortality ratios.
- x_label
Title for the funnel plot x-axis. Usually expected deaths, readmissions, incidents etc.
- y_label
Title for the funnel plot y-axis. Usually a standardised ratio.
- x_range
Manually specify the y-axis min and max, in form c(min, max), e.g. c(0, 200). Default, "auto", allows function to estimate range.
- y_range
Manually specify the y-axis min and max, in form c(min, max), e.g. c(0.7, 1.3). Default, "auto", allows function to estimate range.
- plot_cols
A vector of 8 colours for funnel limits, in order: 95% Poisson (lower/upper), 99.8% Poisson (lower/upper), 95% OD-adjusted (lower/upper), 99.8% OD-adjusted (lower/upper). Default has been chosen to avoid red and green which can lead to subconscious value judgements of good or bad. Default is hex colours: c("#FF7F0EFF", "#FF7F0EFF", "#1F77B4FF","#1F77B4FF", "#9467BDFF", "#9467BDFF", "#2CA02CFF", "#2CA02CFF")
- theme
a ggplot theme function. This can be a canned theme such as theme_bw(), a theme() with arguments, or your own custom theme function. Default is new funnel_clean(), but funnel_classic() is original format.
- label_outliers
Deprecated. Please use the `label` argument instead.
- Poisson_limits
Deprecated. Please use the `draw_unadjusted` argument instead.
- OD_adjust
Deprecated. Please use the `draw_adjusted` argument instead.
- xrange
Deprecated. Please use the `x_range` argument instead.
- yrange
Deprecated. Please use the `y_range` argument instead.
- SHMI_rounding
TRUE/FALSE, for SHMI calculation (standardised ratio, with SHMI truncation etc.), should you round the expected values to 2 decimal places (TRUE) or not (FALSE)
- max.overlaps
Exclude text labels that overlap too many things. Defaults to 10. (inheritted from geom_label_repel)
Value
A fitted `funnelplot` object. A `funnelplot` object is a list containing the following components:
Prints the number of points, outliers and whether the plot has been adjusted, and prints the plot
- plot
A ggplot object with the funnel plot and the appropriate limits
- limits_lookup
A lookup table with selected limits for drawing a plot in software that requires limits.
- aggregated_data
A data.frame of the the aggregated dataset used for the plot.
- outlier
A data frame of outliers from the data.
- tau2
The between-groups standard deviation, \(\tau^2\).
- phi
The dispersion ratio, \(\phi\).
- draw_adjusted
Whether overdispersion-adjusted limits were used.
- draw_unadjusted
Whether unadjusted Poisson limits were used.
Details
Outliers are marked based on the grouping, and the limits chosen, corresponding to either 95% or 99.8% quantiles of the normal distribution.
Labels can attached using the `label` argument.
Overdispersion can be factored in based on the methods in Spiegelhalter et al. (2012), set `draw_adjusted` to FALSE to suppress this.
To use Poisson limits set `draw_unadjusted=TRUE`.
The plot colours deliberately avoid red-amber-green colouring, but you could extract this from the ggplot object and change manually if you like.
Future versions of `funnelplotr` may allow users to change this.
References
DerSimonian & Laird (1986) Meta-analysis in clinical trials. <doi:10.1016/0197-2456(86)90046-2>
Spiegelhalter (2005) Funnel plots for comparing institutional performance <doi:10.1002/sim.1970>
Spiegelhalter et al. (2012) Statistical methods for healthcare regulation: rating, screening and surveillance: <doi:10.1111/j.1467-985X.2011.01010.x>
NHS Digital (2020) SHMI Methodology v .134 https://digital.nhs.uk/data-and-information/publications/ci-hub/summary-hospital-level-mortality-indicator-shmi
Examples
# We will use the 'medpar' dataset from the 'COUNT' package.
# Little reformatting needed
library(COUNT)
#> Loading required package: msme
#> Loading required package: MASS
#> Loading required package: lattice
#> Loading required package: sandwich
data(medpar)
medpar$provnum<-factor(medpar$provnum)
medpar$los<-as.numeric(medpar$los)
mod<- glm(los ~ hmo + died + age80 + factor(type)
, family="poisson", data=medpar)
# Get predicted values for building ratio
medpar$prds<- predict(mod, type="response")
# Draw plot, returning just the plot object
fp<-funnel_plot(medpar, denominator=prds, numerator=los,
group = provnum, limit=95, title="An example funnel plot")
# Methods for viewing/extracting
print(fp)
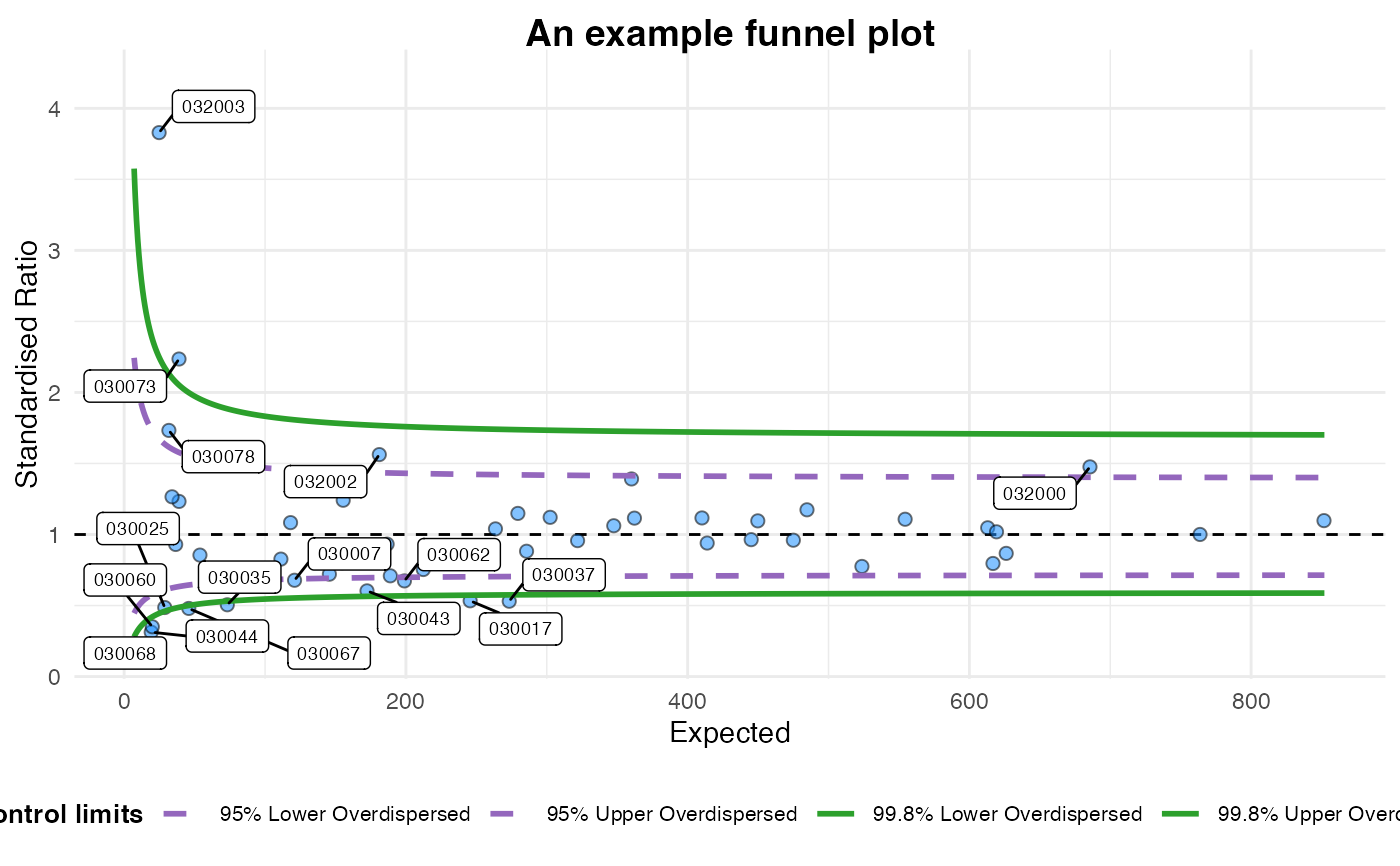#> A funnel plot object with 54 points of which 16 are outliers.
#> Plot is adjusted for overdispersion.
plot(fp)
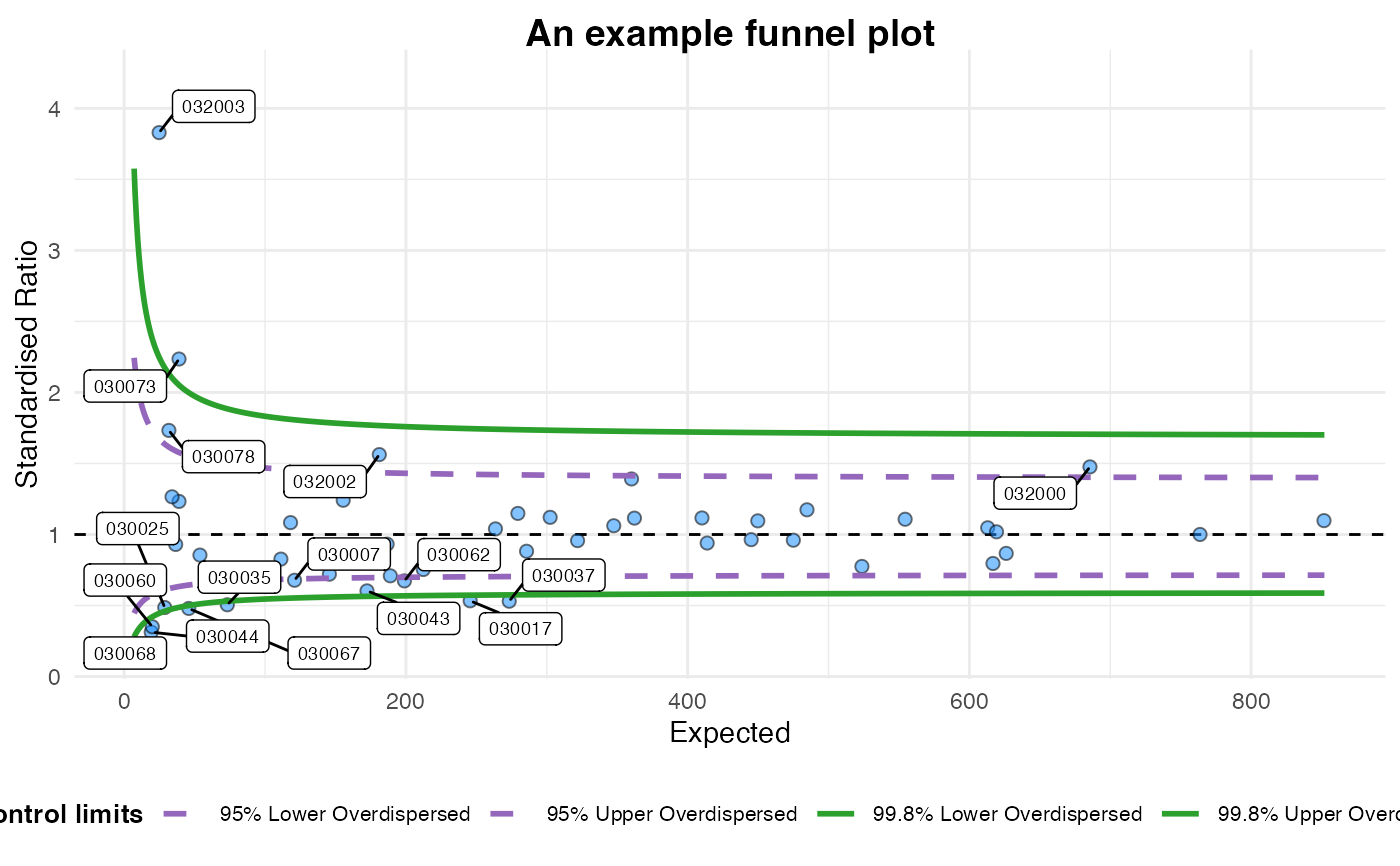summary(fp)
#> A funnel plot object with 54 points of which 16 are outliers.
#> Dispersion ratio: ϕ = 8.532851 .
#> Plot is adjusted for overdispersion. Between unit variance:
#> 𝜏², = 0.02841023 .
#> Outliers:
#> denominator group numerator rr target_transformed Y
#> 17 120.94 030007 82 0.6780368 0 -0.3885753
#> 28 245.61 030017 131 0.5333603 0 -0.6285476
#> 6 28.80 030025 14 0.4861594 0 -0.7213181
#> 14 73.21 030035 37 0.5054258 0 -0.6824141
#> 32 273.34 030037 145 0.5304793 0 -0.6339827
#> 21 172.38 030043 104 0.6033232 0 -0.5053104
#> 3 19.20 030044 6 0.3125609 0 -1.1631508
#> 4 19.96 030060 7 0.3506260 0 -1.0478201
#> 25 198.94 030062 134 0.6735680 0 -0.3951635
#> 12 45.87 030067 22 0.4796652 0 -0.7347689
#> 2 9.67 030068 2 0.2068827 0 -1.5758811
#> 10 38.92 030073 87 2.2352298 0 0.8043999
#> 7 31.74 030078 55 1.7329455 0 0.5497555
#> 52 685.59 032000 1012 1.4761101 0 0.3894041
#> 22 181.11 032002 283 1.5626043 0 0.4463423
#> 5 24.81 032003 95 3.8296445 0 1.3426301
#> Uzscore rk sp truncated Wuzscore s OD95LCL OD95UCL OD99LCL
#> 17 -4.273269 13 2 0 -4.273269 0.09093164 0.6870374 1.455525 0.5533126
#> 28 -9.850566 2 0 1 NA 0.06380827 0.7024099 1.423670 0.5729580
#> 6 -3.870999 16 2 0 -3.870999 0.18633900 0.6111188 1.636343 0.4600330
#> 14 -5.838929 4 0 1 NA 0.11687316 0.6689770 1.494820 0.5305541
#> 32 -10.481634 1 0 1 NA 0.06048510 0.7039943 1.420466 0.5749970
#> 21 -6.634401 3 0 1 NA 0.07616520 0.6959196 1.436948 0.5646331
#> 3 -5.096671 8 1 0 -5.096671 0.22821773 0.5734589 1.743804 0.4161366
#> 4 -4.681306 12 2 0 -4.681306 0.22383074 0.5774252 1.731826 0.4206837
#> 25 -5.573626 7 1 0 -5.573626 0.07089881 0.6987976 1.431030 0.5683191
#> 12 -4.976398 9 1 0 -4.976398 0.14765074 0.6445616 1.551442 0.5003471
#> 2 -4.900458 10 1 0 -4.900458 0.32157832 0.4908522 2.037273 0.3256333
#> 10 5.018321 50 9 1 NA 0.16029264 0.6338819 1.577581 0.4873387
#> 7 3.097227 48 8 0 3.097227 0.17749926 0.6189345 1.615680 0.4693434
#> 52 10.196068 54 9 1 NA 0.03819159 0.7126729 1.403168 0.5862128
#> 22 6.006746 51 9 1 NA 0.07430684 0.6969535 1.434816 0.5659563
#> 5 6.687592 53 9 1 NA 0.20076436 0.5982289 1.671601 0.4448276
#> OD99UCL LCL95 UCL95 LCL99 UCL99 highlight outlier
#> 17 1.807297 0.8297333 1.194925 0.7423709 1.314130 0 1
#> 28 1.745329 0.8788379 1.133198 0.8143570 1.213308 0 1
#> 6 2.173757 0.6686912 1.437947 0.5211690 1.720387 0 1
#> 14 1.884822 0.7841313 1.256939 0.6773325 1.416488 0 1
#> 32 1.739139 0.8849536 1.125850 0.8234590 1.201382 0 1
#> 21 1.771061 0.8562871 1.160931 0.7810534 1.258467 0 1
#> 3 2.403057 0.6038663 1.558062 0.4393444 1.925512 0 1
#> 4 2.377083 0.6104869 1.545079 0.4474921 1.903227 0 1
#> 25 1.759575 0.8658614 1.149033 0.7951428 1.239064 0 1
#> 12 1.998612 0.7317770 1.334400 0.6049421 1.545676 0 1
#> 2 3.070939 0.4725050 1.857410 0.2885378 2.445625 0 1
#> 10 2.051961 0.7108273 1.367468 0.5766906 1.601235 0 1
#> 7 2.130636 0.6828360 1.413670 0.5396094 1.679236 0 1
#> 52 1.705865 0.9265368 1.077739 0.8861228 1.123734 0 1
#> 22 1.766921 0.8596594 1.156719 0.7860075 1.251593 0 1
#> 5 2.248062 0.6459532 1.478364 0.4919575 1.789136 0 1
limits(fp)
#> number.seq s odll95 odul95 odll998 odul998 ll95
#> 1 1.100000 0.95346259 0.1499088 6.670722 0.05018164 19.927608 0.03371131
#> 2 1.951752 0.71579344 0.2366198 4.226189 0.10305763 9.703309 0.11649266
#> 3 2.803504 0.59724077 0.2963262 3.374659 0.14694390 6.805318 0.19111654
#> 4 3.655255 0.52304752 0.3405923 2.936062 0.18301425 5.464055 0.25146337
#> 5 4.507007 0.47103793 0.3751069 2.665907 0.21309812 4.692674 0.30040779
#> 6 5.358759 0.43198423 0.4029908 2.481446 0.23860393 4.191046 0.34084501
#> 7 6.210511 0.40126968 0.4261173 2.346772 0.26054744 3.838073 0.37489241
#> 8 7.062262 0.37629468 0.4456895 2.243714 0.27966440 3.575714 0.40404179
#> 9 7.560000 0.36369648 0.4558174 2.193861 0.28974983 3.451253 0.41924504
#> 10 7.914014 0.35546889 0.4625217 2.162061 0.29649761 3.372708 0.42935482
#> 11 8.765766 0.33775755 0.4771878 2.095611 0.31145585 3.210728 0.45160285
#> 12 9.617518 0.32245455 0.4901059 2.040375 0.32485304 3.078315 0.47135881
#> 13 9.670000 0.32157832 0.4908522 2.037273 0.32563329 3.070939 0.47250496
#> 14 10.469269 0.30905930 0.5015892 1.993663 0.33693458 2.967935 0.48905720
#> 15 11.321021 0.29720575 0.5118776 1.953592 0.34789534 2.874428 0.50503383
#> 16 12.172773 0.28661918 0.5211583 1.918803 0.35789229 2.794137 0.51955264
#> 17 13.024525 0.27708886 0.5295802 1.888288 0.36705342 2.724399 0.53282422
#> 18 13.876276 0.26845008 0.5372631 1.861286 0.37548431 2.663227 0.54501889
#> 19 14.728028 0.26057197 0.5443048 1.837206 0.38327290 2.609107 0.55627603
#> 20 15.579780 0.25334909 0.5507860 1.815587 0.39049313 2.560865 0.56671098
#> 21 16.431532 0.24669536 0.5567740 1.796061 0.39720764 2.517575 0.57642007
#> 22 17.283283 0.24053976 0.5623254 1.778330 0.40346993 2.478499 0.58548452
#> 23 18.135035 0.23482309 0.5674883 1.762151 0.40932599 2.443041 0.59397329
#> 24 18.986787 0.22949555 0.5723037 1.747324 0.41481560 2.410710 0.60194544
#> 25 19.200000 0.22821773 0.5734589 1.743804 0.41613660 2.403057 0.60386634
#> 26 19.838539 0.22451490 0.5768067 1.733683 0.41997337 2.381103 0.60945183
#> 27 19.960000 0.22383074 0.5774252 1.731826 0.42068365 2.377083 0.61048695
#> 28 20.690290 0.21984506 0.5810280 1.721087 0.42482956 2.353885 0.61653653
#> 29 21.542042 0.21545499 0.5849941 1.709419 0.42941075 2.328773 0.62323800
#> 30 22.393794 0.21131784 0.5887283 1.698576 0.43374044 2.305526 0.62958991
#> 31 23.245546 0.20741021 0.5922510 1.688473 0.43783943 2.283942 0.63562192
#> 32 24.097297 0.20371163 0.5955801 1.679035 0.44172624 2.263846 0.64136028
#> 33 24.810000 0.20076436 0.5982289 1.671601 0.44482756 2.248062 0.64595320
#> 34 24.949049 0.20020412 0.5987319 1.670197 0.44541742 2.245085 0.64682829
#> 35 25.800801 0.19687175 0.6017204 1.661902 0.44892779 2.227530 0.65204673
#> 36 26.652553 0.19370043 0.6045583 1.654100 0.45227069 2.211065 0.65703421
#> 37 27.504304 0.19067760 0.6072572 1.646749 0.45545814 2.195591 0.66180745
#> 38 28.356056 0.18779200 0.6098272 1.639809 0.45850102 2.181020 0.66638149
#> 39 28.800000 0.18633900 0.6111188 1.636343 0.46003301 2.173757 0.66869116
#> 40 29.207808 0.18503357 0.6122776 1.633246 0.46140919 2.167274 0.67076995
#> 41 30.059560 0.18239322 0.6146168 1.627030 0.46419161 2.154283 0.67498516
#> 42 30.911311 0.17986277 0.6168524 1.621133 0.46685647 2.141986 0.67903834
#> 43 31.740000 0.17749926 0.6189345 1.615680 0.46934344 2.130636 0.68283598
#> 44 31.763063 0.17743480 0.6189912 1.615532 0.46941123 2.130328 0.68293970
#> 45 32.614815 0.17510258 0.6210395 1.610203 0.47186272 2.119260 0.68669859
#> 46 33.466567 0.17285996 0.6230032 1.605128 0.47421722 2.108738 0.69032353
#> 47 33.980000 0.17154905 0.6241482 1.602184 0.47559209 2.102642 0.69244725
#> 48 34.318318 0.17070137 0.6248874 1.600288 0.47648050 2.098722 0.69382238
#> 49 35.170070 0.16862167 0.6266970 1.595668 0.47865785 2.089175 0.69720235
#> 50 36.021822 0.16661618 0.6284364 1.591251 0.48075417 2.080065 0.70047008
#> 51 36.560000 0.16538530 0.6295011 1.588560 0.48203903 2.074521 0.70247971
#> 52 36.873574 0.16468058 0.6301097 1.587025 0.48277401 2.071363 0.70363169
#> 53 37.725325 0.16281091 0.6317207 1.582978 0.48472153 2.063040 0.70669288
#> 54 38.577077 0.16100351 0.6332728 1.579098 0.48660063 2.055073 0.70965888
#> 55 38.920000 0.16029264 0.6338819 1.577581 0.48733868 2.051961 0.71082726
#> 56 38.930000 0.16027205 0.6338995 1.577537 0.48736005 2.051871 0.71086111
#> 57 39.428829 0.15925499 0.6347694 1.575375 0.48841492 2.047440 0.71253458
#> 58 40.280581 0.15756224 0.6362133 1.571800 0.49016775 2.040118 0.71532450
#> 59 41.132332 0.15592234 0.6376073 1.568363 0.49186223 2.033090 0.71803286
#> 60 41.984084 0.15433259 0.6389541 1.565058 0.49350130 2.026337 0.72066360
#> 61 42.835836 0.15279051 0.6402560 1.561875 0.49508765 2.019844 0.72322038
#> 62 43.687588 0.15129374 0.6415153 1.558809 0.49662384 2.013596 0.72570664
#> 63 44.539339 0.14984012 0.6427341 1.555853 0.49811224 2.007580 0.72812558
#> 64 45.391091 0.14842761 0.6439143 1.553002 0.49955509 2.001781 0.73048022
#> 65 45.870000 0.14765074 0.6445616 1.551442 0.50034713 1.998612 0.73177697
#> 66 46.242843 0.14705430 0.6450577 1.550249 0.50095446 1.996189 0.73277338
#> 67 47.094595 0.14571843 0.6461661 1.547590 0.50231233 1.990793 0.73500770
#> 68 47.946346 0.14441830 0.6472411 1.545019 0.50363054 1.985583 0.73718569
#> 69 48.798098 0.14315237 0.6482842 1.542533 0.50491083 1.980548 0.73930970
#> 70 49.649850 0.14191916 0.6492967 1.540128 0.50615482 1.975680 0.74138192
#> 71 50.501602 0.14071728 0.6502802 1.537799 0.50736406 1.970971 0.74340446
#> 72 51.353353 0.13954542 0.6512357 1.535542 0.50854001 1.966414 0.74537928
#> 73 52.205105 0.13840237 0.6521645 1.533355 0.50968404 1.962000 0.74730824
#> 74 53.056857 0.13728694 0.6530677 1.531235 0.51079744 1.957723 0.74919310
#> 75 53.790000 0.13634814 0.6538255 1.529460 0.51173222 1.954147 0.75078146
#> 76 53.908609 0.13619807 0.6539464 1.529177 0.51188145 1.953577 0.75103554
#> 77 54.760360 0.13513469 0.6548015 1.527180 0.51293722 1.949556 0.75283713
#> 78 55.612112 0.13409584 0.6556341 1.525241 0.51396586 1.945655 0.75459938
#> 79 56.463864 0.13308059 0.6564449 1.523357 0.51496841 1.941867 0.75632370
#> 80 57.315616 0.13208805 0.6572349 1.521526 0.51594587 1.938188 0.75801144
#> 81 58.167367 0.13111739 0.6580049 1.519746 0.51689916 1.934613 0.75966390
#> 82 59.019119 0.13016782 0.6587555 1.518014 0.51782920 1.931139 0.76128230
#> 83 59.870871 0.12923859 0.6594876 1.516329 0.51873682 1.927760 0.76286778
#> 84 60.722623 0.12832898 0.6602018 1.514688 0.51962283 1.924473 0.76442148
#> 85 61.574374 0.12743831 0.6608988 1.513091 0.52048801 1.921274 0.76594444
#> 86 62.426126 0.12656593 0.6615791 1.511535 0.52133308 1.918159 0.76743766
#> 87 63.277878 0.12571122 0.6622435 1.510019 0.52215876 1.915126 0.76890212
#> 88 64.129630 0.12487360 0.6628924 1.508540 0.52296570 1.912171 0.77033873
#> 89 64.981381 0.12405250 0.6635264 1.507099 0.52375453 1.909291 0.77174837
#> 90 65.833133 0.12324739 0.6641460 1.505693 0.52452588 1.906484 0.77313188
#> 91 66.684885 0.12245776 0.6647517 1.504321 0.52528031 1.903745 0.77449005
#> 92 67.536637 0.12168311 0.6653440 1.502982 0.52601839 1.901074 0.77582367
#> 93 68.388388 0.12092297 0.6659233 1.501674 0.52674064 1.898468 0.77713347
#> 94 69.240140 0.12017691 0.6664900 1.500398 0.52744757 1.895923 0.77842015
#> 95 70.091892 0.11944449 0.6670445 1.499150 0.52813967 1.893439 0.77968439
#> 96 70.943644 0.11872529 0.6675873 1.497931 0.52881741 1.891012 0.78092684
#> 97 71.795395 0.11801894 0.6681187 1.496740 0.52948122 1.888641 0.78214813
#> 98 72.647147 0.11732504 0.6686390 1.495575 0.53013154 1.886324 0.78334884
#> 99 73.210000 0.11687316 0.6689770 1.494820 0.53055408 1.884822 0.78413129
#> 100 73.498899 0.11664324 0.6691487 1.494436 0.53076878 1.884060 0.78452956
#> 101 74.350651 0.11597319 0.6696480 1.493322 0.53139332 1.881845 0.78569084
#> 102 75.202402 0.11531456 0.6701372 1.492232 0.53200556 1.879680 0.78683321
#> 103 76.054154 0.11466702 0.6706167 1.491165 0.53260585 1.877561 0.78795719
#> 104 76.905906 0.11403027 0.6710867 1.490120 0.53319454 1.875488 0.78906325
#> 105 77.757658 0.11340401 0.6715476 1.489098 0.53377197 1.873459 0.79015188
#> 106 78.609409 0.11278796 0.6719995 1.488096 0.53433845 1.871473 0.79122354
#> 107 79.461161 0.11218184 0.6724428 1.487115 0.53489431 1.869528 0.79227866
#> 108 80.312913 0.11158538 0.6728777 1.486154 0.53543983 1.867623 0.79331767
#> 109 81.164665 0.11099834 0.6733044 1.485212 0.53597530 1.865758 0.79434097
#> 110 82.016416 0.11042047 0.6737232 1.484289 0.53650101 1.863929 0.79534896
#> 111 82.868168 0.10985154 0.6741342 1.483384 0.53701721 1.862138 0.79634202
#> 112 83.719920 0.10929130 0.6745378 1.482497 0.53752417 1.860381 0.79732053
#> 113 84.571672 0.10873955 0.6749341 1.481626 0.53802214 1.858660 0.79828482
#> 114 85.423423 0.10819608 0.6753232 1.480772 0.53851134 1.856971 0.79923525
#> 115 86.275175 0.10766067 0.6757055 1.479935 0.53899201 1.855315 0.80017214
#> 116 87.126927 0.10713313 0.6760810 1.479113 0.53946438 1.853691 0.80109583
#> 117 87.978679 0.10661327 0.6764500 1.478306 0.53992866 1.852097 0.80200661
#> 118 88.830430 0.10610091 0.6768126 1.477514 0.54038505 1.850532 0.80290478
#> 119 89.682182 0.10559587 0.6771690 1.476736 0.54083376 1.848997 0.80379064
#> 120 90.533934 0.10509796 0.6775193 1.475973 0.54127498 1.847490 0.80466447
#> 121 91.385686 0.10460704 0.6778638 1.475223 0.54170889 1.846010 0.80552654
#> 122 92.237437 0.10412293 0.6782024 1.474486 0.54213568 1.844557 0.80637711
#> 123 93.089189 0.10364548 0.6785355 1.473762 0.54255553 1.843129 0.80721643
#> 124 93.940941 0.10317454 0.6788631 1.473051 0.54296860 1.841727 0.80804476
#> 125 94.792693 0.10270996 0.6791854 1.472352 0.54337505 1.840350 0.80886233
#> 126 95.644444 0.10225160 0.6795024 1.471665 0.54377504 1.838996 0.80966938
#> 127 96.496196 0.10179933 0.6798144 1.470990 0.54416873 1.837665 0.81046612
#> 128 97.347948 0.10135300 0.6801214 1.470326 0.54455627 1.836358 0.81125279
#> 129 98.199700 0.10091249 0.6804236 1.469673 0.54493779 1.835072 0.81202959
#> 130 99.051451 0.10047768 0.6807211 1.469030 0.54531345 1.833808 0.81279672
#> 131 99.903203 0.10004843 0.6810139 1.468399 0.54568337 1.832565 0.81355440
#> 132 100.754955 0.09962465 0.6813022 1.467777 0.54604768 1.831342 0.81430280
#> 133 101.606707 0.09920620 0.6815862 1.467166 0.54640652 1.830139 0.81504213
#> 134 102.458458 0.09879298 0.6818658 1.466564 0.54676000 1.828956 0.81577255
#> 135 103.310210 0.09838488 0.6821412 1.465972 0.54710824 1.827792 0.81649426
#> 136 104.161962 0.09798180 0.6824125 1.465389 0.54745137 1.826646 0.81720742
#> 137 105.013714 0.09758363 0.6826798 1.464816 0.54778948 1.825519 0.81791221
#> 138 105.865465 0.09719028 0.6829432 1.464251 0.54812270 1.824409 0.81860878
#> 139 106.717217 0.09680165 0.6832027 1.463695 0.54845113 1.823316 0.81929730
#> 140 107.568969 0.09641764 0.6834584 1.463147 0.54877487 1.822241 0.81997792
#> 141 108.420721 0.09603817 0.6837105 1.462607 0.54909403 1.821182 0.82065079
#> 142 109.272472 0.09566314 0.6839590 1.462076 0.54940869 1.820139 0.82131605
#> 143 110.124224 0.09529247 0.6842039 1.461553 0.54971895 1.819111 0.82197386
#> 144 110.975976 0.09492607 0.6844454 1.461037 0.55002491 1.818099 0.82262435
#> 145 111.260000 0.09480483 0.6845252 1.460867 0.55012599 1.817765 0.82283966
#> 146 111.827728 0.09456387 0.6846836 1.460529 0.55032665 1.817103 0.82326766
#> 147 112.679479 0.09420579 0.6849184 1.460028 0.55062427 1.816120 0.82390391
#> 148 113.531231 0.09385174 0.6851500 1.459535 0.55091784 1.815153 0.82453324
#> 149 114.382983 0.09350165 0.6853784 1.459048 0.55120744 1.814199 0.82515577
#> 150 115.234735 0.09315546 0.6856037 1.458569 0.55149317 1.813259 0.82577162
#> 151 116.086486 0.09281308 0.6858260 1.458096 0.55177509 1.812333 0.82638092
#> 152 116.938238 0.09247444 0.6860452 1.457630 0.55205329 1.811419 0.82698378
#> 153 117.789990 0.09213949 0.6862616 1.457170 0.55232782 1.810519 0.82758031
#> 154 118.110000 0.09201458 0.6863422 1.456999 0.55243004 1.810184 0.82780282
#> 155 118.641742 0.09180815 0.6864751 1.456717 0.55259878 1.809631 0.82817062
#> 156 119.493493 0.09148036 0.6866858 1.456270 0.55286622 1.808756 0.82875483
#> 157 120.345245 0.09115606 0.6868938 1.455829 0.55313022 1.807893 0.82933303
#> 158 120.940000 0.09093164 0.6870374 1.455525 0.55331256 1.807297 0.82973327
#> 159 121.196997 0.09083518 0.6870990 1.455394 0.55339084 1.807041 0.82990533
#> 160 122.048749 0.09051766 0.6873016 1.454965 0.55364815 1.806201 0.83047183
#> 161 122.900501 0.09020346 0.6875016 1.454542 0.55390220 1.805373 0.83103262
#> 162 123.752252 0.08989250 0.6876991 1.454124 0.55415307 1.804556 0.83158781
#> 163 124.604004 0.08958473 0.6878941 1.453712 0.55440080 1.803749 0.83213749
#> 164 125.455756 0.08928011 0.6880866 1.453305 0.55464546 1.802954 0.83268174
#> 165 126.307508 0.08897857 0.6882767 1.452904 0.55488711 1.802168 0.83322066
#> 166 127.159259 0.08868007 0.6884645 1.452508 0.55512581 1.801393 0.83375433
#> 167 128.011011 0.08838455 0.6886500 1.452117 0.55536159 1.800629 0.83428284
#> 168 128.862763 0.08809196 0.6888331 1.451730 0.55559453 1.799874 0.83480628
#> 169 129.714515 0.08780226 0.6890141 1.451349 0.55582466 1.799129 0.83532471
#> 170 130.566266 0.08751541 0.6891928 1.450973 0.55605205 1.798393 0.83583823
#> 171 131.418018 0.08723134 0.6893695 1.450601 0.55627673 1.797666 0.83634691
#> 172 132.269770 0.08695002 0.6895440 1.450234 0.55649876 1.796949 0.83685082
#> 173 133.121522 0.08667141 0.6897164 1.449871 0.55671819 1.796241 0.83735004
#> 174 133.973273 0.08639546 0.6898868 1.449513 0.55693505 1.795541 0.83784465
#> 175 134.825025 0.08612213 0.6900552 1.449159 0.55714940 1.794851 0.83833471
#> 176 135.676777 0.08585137 0.6902216 1.448810 0.55736128 1.794168 0.83882029
#> 177 136.528529 0.08558316 0.6903861 1.448465 0.55757073 1.793494 0.83930147
#> 178 137.380280 0.08531744 0.6905487 1.448124 0.55777779 1.792829 0.83977830
#> 179 138.232032 0.08505418 0.6907094 1.447787 0.55798251 1.792171 0.84025086
#> 180 139.083784 0.08479334 0.6908683 1.447454 0.55818492 1.791521 0.84071921
#> 181 139.935536 0.08453489 0.6910254 1.447125 0.55838506 1.790879 0.84118340
#> 182 140.787287 0.08427879 0.6911808 1.446800 0.55858297 1.790244 0.84164351
#> 183 141.639039 0.08402500 0.6913344 1.446478 0.55877868 1.789617 0.84209958
#> 184 142.490791 0.08377349 0.6914862 1.446160 0.55897224 1.788998 0.84255169
#> 185 143.342543 0.08352422 0.6916364 1.445846 0.55916368 1.788385 0.84299989
#> 186 144.194294 0.08327717 0.6917850 1.445536 0.55935303 1.787780 0.84344422
#> 187 145.046046 0.08303230 0.6919319 1.445229 0.55954033 1.787181 0.84388476
#> 188 145.670000 0.08285428 0.6920385 1.445006 0.55967626 1.786747 0.84420510
#> 189 145.897798 0.08278957 0.6920772 1.444926 0.55972561 1.786590 0.84432155
#> 190 146.749550 0.08254896 0.6922209 1.444626 0.55990891 1.786005 0.84475465
#> 191 147.601301 0.08231044 0.6923631 1.444329 0.56009025 1.785427 0.84518411
#> 192 148.453053 0.08207397 0.6925038 1.444035 0.56026967 1.784855 0.84560997
#> 193 149.304805 0.08183953 0.6926429 1.443745 0.56044719 1.784289 0.84603230
#> 194 150.156557 0.08160708 0.6927806 1.443458 0.56062285 1.783730 0.84645113
#> 195 151.008308 0.08137661 0.6929168 1.443175 0.56079668 1.783177 0.84686652
#> 196 151.860060 0.08114807 0.6930516 1.442894 0.56096870 1.782631 0.84727852
#> 197 152.711812 0.08092146 0.6931850 1.442616 0.56113894 1.782090 0.84768716
#> 198 153.563564 0.08069672 0.6933170 1.442342 0.56130744 1.781555 0.84809250
#> 199 154.415315 0.08047386 0.6934477 1.442070 0.56147421 1.781026 0.84849458
#> 200 154.660000 0.08041017 0.6934850 1.441992 0.56152180 1.780875 0.84860949
#> 201 155.267067 0.08025282 0.6935770 1.441801 0.56163928 1.780502 0.84889344
#> 202 155.490000 0.08019527 0.6936106 1.441731 0.56168221 1.780366 0.84899731
#> 203 156.118819 0.08003360 0.6937050 1.441535 0.56180269 1.779984 0.84928913
#> 204 156.970571 0.07981617 0.6938316 1.441272 0.56196445 1.779472 0.84968169
#> 205 157.822322 0.07960050 0.6939570 1.441011 0.56212458 1.778965 0.85007116
#> 206 158.674074 0.07938657 0.6940812 1.440754 0.56228313 1.778463 0.85045758
#> 207 159.525826 0.07917435 0.6942040 1.440499 0.56244010 1.777967 0.85084099
#> 208 160.377578 0.07896382 0.6943257 1.440246 0.56259552 1.777476 0.85122142
#> 209 161.229329 0.07875497 0.6944462 1.439996 0.56274941 1.776990 0.85159893
#> 210 162.081081 0.07854777 0.6945654 1.439749 0.56290180 1.776509 0.85197354
#> 211 162.932833 0.07834219 0.6946835 1.439504 0.56305271 1.776033 0.85234529
#> 212 163.784585 0.07813822 0.6948005 1.439262 0.56320216 1.775561 0.85271423
#> 213 164.636336 0.07793583 0.6949163 1.439022 0.56335016 1.775095 0.85308037
#> 214 165.488088 0.07773500 0.6950309 1.438785 0.56349675 1.774633 0.85344377
#> 215 166.339840 0.07753573 0.6951445 1.438550 0.56364195 1.774176 0.85380445
#> 216 167.191592 0.07733797 0.6952570 1.438317 0.56378576 1.773723 0.85416244
#> 217 168.043343 0.07714172 0.6953684 1.438087 0.56392822 1.773275 0.85451779
#> 218 168.895095 0.07694696 0.6954788 1.437858 0.56406933 1.772832 0.85487052
#> 219 169.746847 0.07675367 0.6955881 1.437632 0.56420913 1.772392 0.85522067
#> 220 170.598599 0.07656182 0.6956964 1.437409 0.56434762 1.771958 0.85556826
#> 221 171.450350 0.07637141 0.6958037 1.437187 0.56448483 1.771527 0.85591333
#> 222 172.302102 0.07618241 0.6959099 1.436968 0.56462077 1.771100 0.85625591
#> 223 172.380000 0.07616520 0.6959196 1.436948 0.56463314 1.771061 0.85628712
#> 224 173.153854 0.07599481 0.6960152 1.436750 0.56475547 1.770678 0.85659603
#> 225 174.005606 0.07580858 0.6961195 1.436535 0.56488893 1.770260 0.85693372
#> 226 174.857357 0.07562372 0.6962229 1.436322 0.56502118 1.769845 0.85726900
#> 227 175.709109 0.07544021 0.6963253 1.436110 0.56515223 1.769435 0.85760191
#> 228 176.560861 0.07525802 0.6964268 1.435901 0.56528209 1.769028 0.85793247
#> 229 177.412613 0.07507715 0.6965274 1.435694 0.56541080 1.768626 0.85826072
#> 230 178.264364 0.07489757 0.6966270 1.435488 0.56553835 1.768227 0.85858667
#> 231 179.116116 0.07471928 0.6967258 1.435285 0.56566476 1.767832 0.85891036
#> 232 179.967868 0.07454225 0.6968237 1.435083 0.56579006 1.767440 0.85923181
#> 233 180.819620 0.07436648 0.6969207 1.434884 0.56591425 1.767052 0.85955105
#> 234 181.110000 0.07430684 0.6969535 1.434816 0.56595634 1.766921 0.85965938
#> 235 181.671371 0.07419194 0.6970168 1.434686 0.56603735 1.766668 0.85986809
#> 236 182.523123 0.07401863 0.6971121 1.434490 0.56615938 1.766287 0.86018298
#> 237 183.374875 0.07384653 0.6972066 1.434295 0.56628034 1.765910 0.86049573
#> 238 184.226627 0.07367562 0.6973002 1.434103 0.56640026 1.765536 0.86080636
#> 239 185.078378 0.07350589 0.6973930 1.433912 0.56651914 1.765165 0.86111491
#> 240 185.930130 0.07333733 0.6974850 1.433722 0.56663700 1.764798 0.86142138
#> 241 186.660000 0.07319381 0.6975633 1.433562 0.56673719 1.764486 0.86168238
#> 242 186.781882 0.07316993 0.6975763 1.433535 0.56675385 1.764434 0.86172582
#> 243 187.633634 0.07300366 0.6976667 1.433349 0.56686970 1.764074 0.86202823
#> 244 188.485385 0.07283853 0.6977564 1.433165 0.56698458 1.763716 0.86232864
#> 245 188.930000 0.07275277 0.6978029 1.433069 0.56704416 1.763531 0.86248467
#> 246 189.337137 0.07267451 0.6978453 1.432982 0.56709848 1.763362 0.86262708
#> 247 190.188889 0.07251159 0.6979334 1.432801 0.56721143 1.763011 0.86292357
#> 248 191.040641 0.07234976 0.6980208 1.432622 0.56732343 1.762663 0.86321812
#> 249 191.892392 0.07218902 0.6981075 1.432444 0.56743449 1.762318 0.86351075
#> 250 192.744144 0.07202933 0.6981934 1.432268 0.56754464 1.761976 0.86380150
#> 251 193.595896 0.07187071 0.6982787 1.432093 0.56765387 1.761637 0.86409037
#> 252 194.447648 0.07171313 0.6983632 1.431920 0.56776220 1.761301 0.86437740
#> 253 195.299399 0.07155658 0.6984470 1.431748 0.56786965 1.760968 0.86466259
#> 254 196.151151 0.07140105 0.6985301 1.431577 0.56797621 1.760637 0.86494597
#> 255 197.002903 0.07124653 0.6986126 1.431409 0.56808191 1.760310 0.86522756
#> 256 197.854655 0.07109300 0.6986943 1.431241 0.56818676 1.759985 0.86550737
#> 257 198.706406 0.07094047 0.6987755 1.431075 0.56829076 1.759663 0.86578543
#> 258 198.940000 0.07089881 0.6987976 1.431030 0.56831913 1.759575 0.86586138
#> 259 199.558158 0.07078892 0.6988559 1.430910 0.56839392 1.759343 0.86606175
#> 260 200.409910 0.07063833 0.6989357 1.430747 0.56849626 1.759027 0.86633635
#> 261 201.261662 0.07048870 0.6990149 1.430585 0.56859778 1.758712 0.86660926
#> 262 202.113413 0.07034001 0.6990934 1.430424 0.56869849 1.758401 0.86688047
#> 263 202.965165 0.07019226 0.6991713 1.430265 0.56879841 1.758092 0.86715003
#> 264 203.816917 0.07004544 0.6992486 1.430107 0.56889754 1.757786 0.86741793
#> 265 204.668669 0.06989954 0.6993252 1.429950 0.56899589 1.757482 0.86768420
#> 266 205.520420 0.06975454 0.6994013 1.429794 0.56909348 1.757181 0.86794886
#> 267 206.372172 0.06961045 0.6994768 1.429640 0.56919031 1.756882 0.86821191
#> 268 207.223924 0.06946724 0.6995517 1.429487 0.56928638 1.756585 0.86847338
#> 269 208.075676 0.06932491 0.6996260 1.429335 0.56938171 1.756291 0.86873329
#> 270 208.927427 0.06918346 0.6996997 1.429185 0.56947631 1.755999 0.86899164
#> 271 209.779179 0.06904287 0.6997728 1.429035 0.56957018 1.755710 0.86924846
#> 272 210.630931 0.06890313 0.6998454 1.428887 0.56966334 1.755423 0.86950376
#> 273 211.482683 0.06876423 0.6999175 1.428740 0.56975579 1.755138 0.86975755
#> 274 212.334434 0.06862617 0.6999889 1.428594 0.56984754 1.754855 0.87000985
#> 275 212.340000 0.06862527 0.6999894 1.428593 0.56984814 1.754854 0.87001149
#> 276 213.186186 0.06848894 0.7000599 1.428449 0.56993859 1.754575 0.87026067
#> 277 214.037938 0.06835253 0.7001303 1.428306 0.57002896 1.754297 0.87051003
#> 278 214.889690 0.06821694 0.7002001 1.428163 0.57011866 1.754021 0.87075795
#> 279 215.741441 0.06808214 0.7002695 1.428022 0.57020768 1.753747 0.87100443
#> 280 216.593193 0.06794814 0.7003383 1.427881 0.57029604 1.753475 0.87124949
#> 281 217.444945 0.06781493 0.7004066 1.427742 0.57038375 1.753206 0.87149314
#> 282 218.296697 0.06768250 0.7004744 1.427604 0.57047081 1.752938 0.87173540
#> 283 219.148448 0.06755085 0.7005417 1.427467 0.57055723 1.752673 0.87197628
#> 284 220.000200 0.06741996 0.7006085 1.427331 0.57064302 1.752409 0.87221579
#> 285 220.851952 0.06728982 0.7006748 1.427196 0.57072818 1.752148 0.87245395
#> 286 221.703704 0.06716044 0.7007407 1.427061 0.57081272 1.751888 0.87269077
#> 287 222.555455 0.06703180 0.7008060 1.426928 0.57089665 1.751631 0.87292626
#> 288 223.407207 0.06690390 0.7008709 1.426796 0.57097997 1.751375 0.87316044
#> 289 224.258959 0.06677672 0.7009353 1.426665 0.57106270 1.751121 0.87339331
#> 290 225.110711 0.06665027 0.7009992 1.426535 0.57114483 1.750869 0.87362489
#> 291 225.962462 0.06652454 0.7010627 1.426406 0.57122637 1.750619 0.87385519
#> 292 226.814214 0.06639951 0.7011257 1.426278 0.57130733 1.750371 0.87408422
#> 293 227.665966 0.06627518 0.7011883 1.426150 0.57138772 1.750125 0.87431200
#> 294 228.517718 0.06615156 0.7012504 1.426024 0.57146754 1.749881 0.87453853
#> 295 229.369469 0.06602862 0.7013121 1.425899 0.57154680 1.749638 0.87476383
#> 296 230.221221 0.06590636 0.7013734 1.425774 0.57162551 1.749397 0.87498791
#> 297 231.072973 0.06578478 0.7014342 1.425651 0.57170366 1.749158 0.87521077
#> 298 231.924725 0.06566387 0.7014946 1.425528 0.57178127 1.748921 0.87543244
#> 299 232.776476 0.06554362 0.7015545 1.425406 0.57185833 1.748685 0.87565291
#> 300 233.628228 0.06542404 0.7016141 1.425285 0.57193487 1.748451 0.87587221
#> 301 234.479980 0.06530510 0.7016732 1.425165 0.57201088 1.748219 0.87609034
#> 302 235.331732 0.06518681 0.7017319 1.425046 0.57208636 1.747988 0.87630731
#> 303 236.183483 0.06506917 0.7017903 1.424927 0.57216133 1.747759 0.87652313
#> 304 237.035235 0.06495215 0.7018482 1.424810 0.57223579 1.747531 0.87673782
#> 305 237.886987 0.06483577 0.7019057 1.424693 0.57230974 1.747306 0.87695138
#> 306 238.738739 0.06472001 0.7019628 1.424577 0.57238319 1.747081 0.87716382
#> 307 239.590490 0.06460486 0.7020196 1.424462 0.57245614 1.746859 0.87737515
#> 308 240.442242 0.06449033 0.7020759 1.424347 0.57252861 1.746638 0.87758539
#> 309 241.293994 0.06437641 0.7021319 1.424234 0.57260058 1.746418 0.87779453
#> 310 242.030000 0.06427845 0.7021800 1.424136 0.57266239 1.746230 0.87797439
#> 311 242.145746 0.06426309 0.7021875 1.424121 0.57267208 1.746200 0.87800260
#> 312 242.997497 0.06415036 0.7022428 1.424009 0.57274309 1.745984 0.87820960
#> 313 243.849249 0.06403823 0.7022976 1.423898 0.57281364 1.745768 0.87841553
#> 314 244.701001 0.06392668 0.7023521 1.423787 0.57288372 1.745555 0.87862042
#> 315 245.552753 0.06381571 0.7024062 1.423678 0.57295334 1.745343 0.87882426
#> 316 245.610000 0.06380827 0.7024099 1.423670 0.57295800 1.745329 0.87883792
#> 317 246.404505 0.06370532 0.7024600 1.423569 0.57302249 1.745132 0.87902707
#> 318 247.256256 0.06359550 0.7025134 1.423460 0.57309120 1.744923 0.87922885
#> 319 248.108008 0.06348624 0.7025665 1.423353 0.57315946 1.744715 0.87942962
#> 320 248.959760 0.06337755 0.7026192 1.423246 0.57322727 1.744509 0.87962937
#> 321 249.811512 0.06326941 0.7026716 1.423140 0.57329464 1.744304 0.87982813
#> 322 250.190000 0.06322153 0.7026948 1.423093 0.57332444 1.744213 0.87991614
#> 323 250.663263 0.06316182 0.7027236 1.423035 0.57336158 1.744100 0.88002590
#> 324 251.515015 0.06305478 0.7027753 1.422930 0.57342808 1.743898 0.88022268
#> 325 252.366767 0.06294829 0.7028267 1.422826 0.57349416 1.743697 0.88041849
#> 326 253.218519 0.06284233 0.7028777 1.422723 0.57355981 1.743497 0.88061334
#> 327 254.070270 0.06273690 0.7029284 1.422620 0.57362504 1.743299 0.88080722
#> 328 254.922022 0.06263201 0.7029788 1.422518 0.57368986 1.743102 0.88100015
#> 329 255.650000 0.06254277 0.7030216 1.422431 0.57374493 1.742935 0.88116430
#> 330 255.773774 0.06252763 0.7030288 1.422417 0.57375427 1.742906 0.88119214
#> 331 256.625526 0.06242378 0.7030786 1.422316 0.57381827 1.742712 0.88138320
#> 332 257.477277 0.06232045 0.7031280 1.422216 0.57388186 1.742519 0.88157332
#> 333 258.329029 0.06221762 0.7031771 1.422117 0.57394506 1.742327 0.88176253
#> 334 259.180781 0.06211530 0.7032259 1.422018 0.57400786 1.742136 0.88195082
#> 335 260.032533 0.06201349 0.7032744 1.421920 0.57407027 1.741947 0.88213821
#> 336 260.884284 0.06191217 0.7033226 1.421823 0.57413229 1.741759 0.88232470
#> 337 261.736036 0.06181135 0.7033705 1.421726 0.57419392 1.741572 0.88251029
#> 338 262.587788 0.06171102 0.7034181 1.421630 0.57425517 1.741386 0.88269501
#> 339 263.439540 0.06161118 0.7034653 1.421534 0.57431605 1.741202 0.88287884
#> 340 263.560000 0.06159710 0.7034720 1.421521 0.57432463 1.741176 0.88290477
#> 341 264.291291 0.06151182 0.7035123 1.421439 0.57437655 1.741018 0.88306181
#> 342 265.143043 0.06141294 0.7035591 1.421345 0.57443668 1.740836 0.88324392
#> 343 265.994795 0.06131453 0.7036055 1.421251 0.57449644 1.740655 0.88342516
#> 344 266.846547 0.06121660 0.7036516 1.421158 0.57455584 1.740475 0.88360556
#> 345 267.698298 0.06111913 0.7036975 1.421065 0.57461487 1.740296 0.88378511
#> 346 268.550050 0.06102213 0.7037431 1.420973 0.57467355 1.740118 0.88396383
#> 347 269.401802 0.06092559 0.7037884 1.420882 0.57473187 1.739942 0.88414172
#> 348 270.253554 0.06082951 0.7038334 1.420791 0.57478985 1.739766 0.88431878
#> 349 271.105305 0.06073388 0.7038781 1.420700 0.57484747 1.739592 0.88449503
#> 350 271.957057 0.06063869 0.7039226 1.420611 0.57490475 1.739419 0.88467047
#> 351 272.808809 0.06054396 0.7039668 1.420521 0.57496169 1.739246 0.88484510
#> 352 273.340000 0.06048510 0.7039943 1.420466 0.57499703 1.739139 0.88495360
#> 353 273.660561 0.06044966 0.7040108 1.420433 0.57501829 1.739075 0.88501893
#> 354 274.512312 0.06035581 0.7040545 1.420345 0.57507455 1.738905 0.88519197
#> 355 275.364064 0.06026239 0.7040979 1.420257 0.57513049 1.738736 0.88536423
#> 356 276.215816 0.06016941 0.7041411 1.420170 0.57518609 1.738568 0.88553570
#> 357 277.067568 0.06007685 0.7041840 1.420083 0.57524136 1.738401 0.88570640
#> 358 277.919319 0.05998472 0.7042267 1.419997 0.57529631 1.738235 0.88587633
#> 359 278.771071 0.05989301 0.7042691 1.419912 0.57535094 1.738070 0.88604550
#> 360 279.480000 0.05981700 0.7043042 1.419841 0.57539617 1.737933 0.88618572
#> 361 279.622823 0.05980172 0.7043112 1.419827 0.57540525 1.737906 0.88621391
#> 362 280.474575 0.05971085 0.7043531 1.419742 0.57545925 1.737743 0.88638157
#> 363 281.326326 0.05962039 0.7043948 1.419658 0.57551293 1.737580 0.88654848
#> 364 282.178078 0.05953034 0.7044362 1.419575 0.57556630 1.737419 0.88671465
#> 365 283.029830 0.05944070 0.7044774 1.419492 0.57561937 1.737259 0.88688009
#> 366 283.881582 0.05935146 0.7045184 1.419409 0.57567213 1.737100 0.88704480
#> 367 284.733333 0.05926262 0.7045591 1.419327 0.57572459 1.736942 0.88720878
#> 368 285.585085 0.05917418 0.7045996 1.419246 0.57577674 1.736784 0.88737205
#> 369 285.640000 0.05916849 0.7046022 1.419241 0.57578010 1.736774 0.88738255
#> 370 286.436837 0.05908613 0.7046398 1.419165 0.57582860 1.736628 0.88753460
#> 371 287.288589 0.05899848 0.7046799 1.419084 0.57588017 1.736472 0.88769644
#> 372 288.140340 0.05891121 0.7047197 1.419004 0.57593145 1.736318 0.88785758
#> 373 288.992092 0.05882433 0.7047592 1.418924 0.57598243 1.736164 0.88801802
#> 374 289.843844 0.05873784 0.7047986 1.418845 0.57603313 1.736011 0.88817777
#> 375 290.695596 0.05865172 0.7048377 1.418766 0.57608354 1.735859 0.88833683
#> 376 291.547347 0.05856599 0.7048766 1.418688 0.57613367 1.735708 0.88849521
#> 377 292.399099 0.05848062 0.7049153 1.418610 0.57618353 1.735558 0.88865291
#> 378 293.250851 0.05839563 0.7049537 1.418533 0.57623310 1.735409 0.88880993
#> 379 294.102603 0.05831101 0.7049920 1.418456 0.57628240 1.735260 0.88896629
#> 380 294.954354 0.05822676 0.7050300 1.418379 0.57633142 1.735113 0.88912198
#> 381 295.806106 0.05814287 0.7050679 1.418303 0.57638018 1.734966 0.88927701
#> 382 296.657858 0.05805934 0.7051055 1.418228 0.57642867 1.734820 0.88943139
#> 383 297.509610 0.05797617 0.7051429 1.418152 0.57647689 1.734675 0.88958512
#> 384 298.361361 0.05789335 0.7051801 1.418077 0.57652484 1.734531 0.88973821
#> 385 299.213113 0.05781089 0.7052171 1.418003 0.57657254 1.734387 0.88989065
#> 386 300.064865 0.05772879 0.7052539 1.417929 0.57661997 1.734244 0.89004246
#> 387 300.916617 0.05764703 0.7052905 1.417856 0.57666715 1.734103 0.89019363
#> 388 301.768368 0.05756561 0.7053269 1.417782 0.57671407 1.733962 0.89034418
#> 389 302.390000 0.05750641 0.7053533 1.417729 0.57674815 1.733859 0.89045366
#> 390 302.620120 0.05748455 0.7053631 1.417710 0.57676074 1.733821 0.89049410
#> 391 303.471872 0.05740382 0.7053991 1.417637 0.57680715 1.733682 0.89064341
#> 392 304.323624 0.05732343 0.7054349 1.417565 0.57685332 1.733543 0.89079210
#> 393 305.175375 0.05724338 0.7054705 1.417494 0.57689924 1.733405 0.89094018
#> 394 306.027127 0.05716366 0.7055059 1.417423 0.57694491 1.733268 0.89108765
#> 395 306.878879 0.05708428 0.7055412 1.417352 0.57699035 1.733131 0.89123452
#> 396 307.730631 0.05700522 0.7055762 1.417281 0.57703553 1.732996 0.89138080
#> 397 308.582382 0.05692649 0.7056111 1.417211 0.57708048 1.732861 0.89152648
#> 398 309.434134 0.05684809 0.7056457 1.417142 0.57712520 1.732726 0.89167157
#> 399 310.285886 0.05677001 0.7056802 1.417072 0.57716967 1.732593 0.89181607
#> 400 311.137638 0.05669225 0.7057145 1.417004 0.57721392 1.732460 0.89195999
#> 401 311.989389 0.05661481 0.7057487 1.416935 0.57725793 1.732328 0.89210334
#> 402 312.841141 0.05653769 0.7057826 1.416867 0.57730171 1.732197 0.89224611
#> 403 313.692893 0.05646088 0.7058164 1.416799 0.57734526 1.732066 0.89238831
#> 404 314.544645 0.05638439 0.7058500 1.416732 0.57738858 1.731936 0.89252994
#> 405 315.396396 0.05630820 0.7058834 1.416665 0.57743168 1.731807 0.89267101
#> 406 316.248148 0.05623232 0.7059166 1.416598 0.57747456 1.731678 0.89281152
#> 407 317.099900 0.05615675 0.7059497 1.416531 0.57751722 1.731550 0.89295148
#> 408 317.951652 0.05608148 0.7059826 1.416465 0.57755965 1.731423 0.89309088
#> 409 318.803403 0.05600651 0.7060153 1.416400 0.57760187 1.731296 0.89322974
#> 410 319.655155 0.05593184 0.7060479 1.416334 0.57764387 1.731170 0.89336805
#> 411 320.506907 0.05585748 0.7060803 1.416270 0.57768566 1.731045 0.89350582
#> 412 321.358659 0.05578340 0.7061125 1.416205 0.57772723 1.730921 0.89364305
#> 413 321.860000 0.05573994 0.7061314 1.416167 0.57775160 1.730848 0.89372358
#> 414 322.210410 0.05570962 0.7061446 1.416141 0.57776859 1.730797 0.89377975
#> 415 323.062162 0.05563614 0.7061765 1.416077 0.57780975 1.730673 0.89391592
#> 416 323.913914 0.05556294 0.7062082 1.416013 0.57785069 1.730551 0.89405156
#> 417 324.765666 0.05549003 0.7062398 1.415950 0.57789143 1.730429 0.89418668
#> 418 325.617417 0.05541741 0.7062712 1.415887 0.57793196 1.730307 0.89432128
#> 419 326.469169 0.05534507 0.7063025 1.415824 0.57797229 1.730187 0.89445536
#> 420 327.320921 0.05527301 0.7063336 1.415762 0.57801242 1.730067 0.89458893
#> 421 328.172673 0.05520123 0.7063645 1.415700 0.57805234 1.729947 0.89472198
#> 422 329.024424 0.05512974 0.7063953 1.415638 0.57809207 1.729828 0.89485453
#> 423 329.876176 0.05505852 0.7064260 1.415577 0.57813160 1.729710 0.89498658
#> 424 330.727928 0.05498757 0.7064564 1.415515 0.57817093 1.729592 0.89511813
#> 425 331.579680 0.05491690 0.7064868 1.415455 0.57821007 1.729475 0.89524918
#> 426 332.431431 0.05484651 0.7065169 1.415394 0.57824902 1.729359 0.89537973
#> 427 333.283183 0.05477638 0.7065470 1.415334 0.57828777 1.729243 0.89550979
#> 428 334.134935 0.05470652 0.7065769 1.415274 0.57832634 1.729128 0.89563937
#> 429 334.986687 0.05463692 0.7066066 1.415215 0.57836471 1.729013 0.89576846
#> 430 335.838438 0.05456759 0.7066362 1.415155 0.57840290 1.728899 0.89589707
#> 431 336.690190 0.05449853 0.7066656 1.415096 0.57844090 1.728785 0.89602519
#> 432 337.541942 0.05442972 0.7066949 1.415038 0.57847872 1.728672 0.89615285
#> 433 338.393694 0.05436118 0.7067241 1.414979 0.57851635 1.728560 0.89628003
#> 434 339.245445 0.05429289 0.7067531 1.414921 0.57855381 1.728448 0.89640674
#> 435 340.097197 0.05422486 0.7067820 1.414863 0.57859108 1.728336 0.89653298
#> 436 340.948949 0.05415709 0.7068107 1.414806 0.57862817 1.728226 0.89665876
#> 437 341.800701 0.05408957 0.7068393 1.414749 0.57866508 1.728115 0.89678407
#> 438 342.652452 0.05402230 0.7068678 1.414692 0.57870182 1.728006 0.89690893
#> 439 343.504204 0.05395528 0.7068961 1.414635 0.57873838 1.727896 0.89703333
#> 440 344.355956 0.05388851 0.7069243 1.414579 0.57877476 1.727788 0.89715728
#> 441 345.207708 0.05382199 0.7069523 1.414522 0.57881098 1.727680 0.89728078
#> 442 346.059459 0.05375571 0.7069803 1.414467 0.57884702 1.727572 0.89740383
#> 443 346.911211 0.05368968 0.7070081 1.414411 0.57888289 1.727465 0.89752643
#> 444 347.540000 0.05364109 0.7070285 1.414370 0.57890926 1.727386 0.89761666
#> 445 347.762963 0.05362389 0.7070357 1.414356 0.57891859 1.727359 0.89764860
#> 446 348.614715 0.05355834 0.7070632 1.414301 0.57895412 1.727253 0.89777032
#> 447 349.466466 0.05349304 0.7070906 1.414246 0.57898949 1.727147 0.89789161
#> 448 350.318218 0.05342797 0.7071179 1.414191 0.57902469 1.727042 0.89801246
#> 449 351.169970 0.05336313 0.7071450 1.414137 0.57905972 1.726938 0.89813288
#> 450 352.021722 0.05329853 0.7071720 1.414083 0.57909459 1.726834 0.89825287
#> 451 352.873473 0.05323417 0.7071989 1.414029 0.57912930 1.726730 0.89837244
#> 452 353.725225 0.05317004 0.7072257 1.413976 0.57916385 1.726627 0.89849158
#> 453 354.576977 0.05310614 0.7072523 1.413923 0.57919824 1.726525 0.89861030
#> 454 355.428729 0.05304247 0.7072788 1.413870 0.57923246 1.726423 0.89872860
#> 455 356.280480 0.05297903 0.7073052 1.413817 0.57926653 1.726321 0.89884648
#> 456 357.132232 0.05291581 0.7073315 1.413764 0.57930045 1.726220 0.89896395
#> 457 357.983984 0.05285282 0.7073576 1.413712 0.57933420 1.726119 0.89908101
#> 458 358.835736 0.05279006 0.7073836 1.413660 0.57936781 1.726019 0.89919765
#> 459 359.687487 0.05272752 0.7074095 1.413608 0.57940126 1.725920 0.89931390
#> 460 360.150000 0.05269365 0.7074235 1.413580 0.57941936 1.725866 0.89937685
#> 461 360.539239 0.05266520 0.7074353 1.413557 0.57943455 1.725820 0.89942973
#> 462 361.390991 0.05260310 0.7074610 1.413506 0.57946770 1.725722 0.89954517
#> 463 362.220000 0.05254287 0.7074858 1.413456 0.57949981 1.725626 0.89965713
#> 464 362.242743 0.05254122 0.7074865 1.413454 0.57950069 1.725623 0.89966020
#> 465 363.094494 0.05247956 0.7075120 1.413404 0.57953354 1.725526 0.89977484
#> 466 363.946246 0.05241811 0.7075373 1.413353 0.57956623 1.725428 0.89988908
#> 467 364.797998 0.05235688 0.7075625 1.413303 0.57959878 1.725331 0.90000293
#> 468 365.649750 0.05229587 0.7075876 1.413253 0.57963119 1.725235 0.90011639
#> 469 366.501502 0.05223506 0.7076125 1.413203 0.57966344 1.725139 0.90022945
#> 470 367.353253 0.05217447 0.7076374 1.413153 0.57969556 1.725043 0.90034214
#> 471 368.205005 0.05211409 0.7076622 1.413104 0.57972752 1.724948 0.90045444
#> 472 369.056757 0.05205392 0.7076868 1.413054 0.57975935 1.724854 0.90056635
#> 473 369.908509 0.05199395 0.7077113 1.413006 0.57979104 1.724759 0.90067789
#> 474 370.760260 0.05193420 0.7077357 1.412957 0.57982258 1.724666 0.90078905
#> 475 371.612012 0.05187464 0.7077601 1.412908 0.57985398 1.724572 0.90089983
#> 476 372.463764 0.05181530 0.7077843 1.412860 0.57988525 1.724479 0.90101024
#> 477 373.315516 0.05175615 0.7078084 1.412812 0.57991638 1.724387 0.90112028
#> 478 374.167267 0.05169721 0.7078323 1.412764 0.57994737 1.724294 0.90122995
#> 479 375.019019 0.05163847 0.7078562 1.412716 0.57997822 1.724203 0.90133926
#> 480 375.870771 0.05157993 0.7078800 1.412669 0.58000894 1.724111 0.90144819
#> 481 376.722523 0.05152158 0.7079037 1.412622 0.58003953 1.724020 0.90155677
#> 482 377.574274 0.05146344 0.7079273 1.412575 0.58006998 1.723930 0.90166498
#> 483 378.426026 0.05140549 0.7079507 1.412528 0.58010030 1.723840 0.90177284
#> 484 379.277778 0.05134774 0.7079741 1.412481 0.58013048 1.723750 0.90188033
#> 485 380.129530 0.05129018 0.7079974 1.412435 0.58016054 1.723661 0.90198748
#> 486 380.981281 0.05123281 0.7080205 1.412388 0.58019047 1.723572 0.90209427
#> 487 381.833033 0.05117564 0.7080436 1.412342 0.58022026 1.723483 0.90220071
#> 488 382.684785 0.05111865 0.7080665 1.412297 0.58024993 1.723395 0.90230680
#> 489 383.536537 0.05106186 0.7080894 1.412251 0.58027947 1.723308 0.90241254
#> 490 384.388288 0.05100526 0.7081122 1.412206 0.58030889 1.723220 0.90251793
#> 491 385.240040 0.05094884 0.7081348 1.412160 0.58033818 1.723133 0.90262299
#> 492 386.091792 0.05089261 0.7081574 1.412115 0.58036734 1.723047 0.90272770
#> 493 386.943544 0.05083656 0.7081799 1.412071 0.58039638 1.722960 0.90283207
#> 494 387.795295 0.05078071 0.7082023 1.412026 0.58042529 1.722875 0.90293610
#> 495 388.647047 0.05072503 0.7082245 1.411982 0.58045409 1.722789 0.90303980
#> 496 389.498799 0.05066954 0.7082467 1.411937 0.58048276 1.722704 0.90314316
#> 497 390.350551 0.05061423 0.7082688 1.411893 0.58051131 1.722619 0.90324619
#> 498 391.202302 0.05055910 0.7082908 1.411849 0.58053974 1.722535 0.90334889
#> 499 392.054054 0.05050415 0.7083127 1.411806 0.58056805 1.722451 0.90345126
#> 500 392.905806 0.05044937 0.7083345 1.411762 0.58059624 1.722367 0.90355331
#> 501 393.757558 0.05039478 0.7083563 1.411719 0.58062431 1.722284 0.90365503
#> 502 394.609309 0.05034036 0.7083779 1.411676 0.58065227 1.722201 0.90375642
#> 503 395.461061 0.05028612 0.7083994 1.411633 0.58068011 1.722119 0.90385749
#> 504 396.312813 0.05023205 0.7084209 1.411590 0.58070783 1.722036 0.90395825
#> 505 397.164565 0.05017816 0.7084422 1.411548 0.58073544 1.721954 0.90405868
#> 506 398.016316 0.05012444 0.7084635 1.411505 0.58076293 1.721873 0.90415880
#> 507 398.868068 0.05007090 0.7084847 1.411463 0.58079031 1.721792 0.90425860
#> 508 399.719820 0.05001752 0.7085058 1.411421 0.58081758 1.721711 0.90435808
#> 509 400.571572 0.04996432 0.7085268 1.411379 0.58084474 1.721630 0.90445726
#> 510 401.423323 0.04991128 0.7085477 1.411338 0.58087178 1.721550 0.90455612
#> 511 402.275075 0.04985841 0.7085686 1.411296 0.58089871 1.721471 0.90465468
#> 512 403.126827 0.04980571 0.7085893 1.411255 0.58092553 1.721391 0.90475293
#> 513 403.978579 0.04975318 0.7086100 1.411214 0.58095224 1.721312 0.90485087
#> 514 404.830330 0.04970081 0.7086306 1.411173 0.58097885 1.721233 0.90494851
#> 515 405.682082 0.04964861 0.7086511 1.411132 0.58100534 1.721155 0.90504585
#> 516 406.533834 0.04959657 0.7086715 1.411091 0.58103173 1.721076 0.90514289
#> 517 407.385586 0.04954470 0.7086918 1.411051 0.58105801 1.720999 0.90523963
#> 518 408.237337 0.04949298 0.7087120 1.411010 0.58108418 1.720921 0.90533607
#> 519 409.089089 0.04944143 0.7087322 1.410970 0.58111025 1.720844 0.90543221
#> 520 409.940841 0.04939004 0.7087523 1.410930 0.58113622 1.720767 0.90552806
#> 521 410.160000 0.04937685 0.7087574 1.410920 0.58114288 1.720747 0.90555267
#> 522 410.792593 0.04933881 0.7087723 1.410890 0.58116207 1.720690 0.90562361
#> 523 411.644344 0.04928774 0.7087922 1.410851 0.58118783 1.720614 0.90571888
#> 524 412.496096 0.04923683 0.7088121 1.410811 0.58121348 1.720538 0.90581385
#> 525 413.347848 0.04918607 0.7088318 1.410772 0.58123903 1.720463 0.90590854
#> 526 413.860000 0.04915563 0.7088437 1.410748 0.58125434 1.720417 0.90596533
#> 527 414.199600 0.04913548 0.7088515 1.410733 0.58126448 1.720387 0.90600294
#> 528 415.051351 0.04908503 0.7088711 1.410694 0.58128983 1.720312 0.90609705
#> 529 415.903103 0.04903474 0.7088906 1.410655 0.58131507 1.720238 0.90619088
#> 530 416.754855 0.04898461 0.7089101 1.410616 0.58134022 1.720163 0.90628442
#> 531 417.606607 0.04893463 0.7089295 1.410578 0.58136526 1.720089 0.90637769
#> 532 418.458358 0.04888480 0.7089487 1.410539 0.58139021 1.720015 0.90647067
#> 533 419.310110 0.04883513 0.7089680 1.410501 0.58141506 1.719942 0.90656337
#> 534 420.161862 0.04878560 0.7089871 1.410463 0.58143981 1.719868 0.90665580
#> 535 421.013614 0.04873623 0.7090062 1.410425 0.58146446 1.719796 0.90674795
#> 536 421.865365 0.04868701 0.7090252 1.410387 0.58148902 1.719723 0.90683983
#> 537 422.717117 0.04863793 0.7090441 1.410350 0.58151348 1.719651 0.90693143
#> 538 423.568869 0.04858900 0.7090629 1.410312 0.58153785 1.719579 0.90702277
#> 539 424.420621 0.04854022 0.7090817 1.410275 0.58156212 1.719507 0.90711383
#> 540 425.272372 0.04849159 0.7091004 1.410238 0.58158630 1.719435 0.90720462
#> 541 426.124124 0.04844310 0.7091190 1.410201 0.58161038 1.719364 0.90729515
#> 542 426.975876 0.04839476 0.7091376 1.410164 0.58163437 1.719293 0.90738541
#> 543 427.827628 0.04834656 0.7091560 1.410127 0.58165826 1.719223 0.90747540
#> 544 428.679379 0.04829851 0.7091745 1.410090 0.58168207 1.719152 0.90756513
#> 545 429.531131 0.04825060 0.7091928 1.410054 0.58170578 1.719082 0.90765459
#> 546 430.382883 0.04820283 0.7092111 1.410018 0.58172940 1.719012 0.90774380
#> 547 431.234635 0.04815520 0.7092292 1.409981 0.58175293 1.718943 0.90783275
#> 548 432.086386 0.04810771 0.7092474 1.409945 0.58177638 1.718874 0.90792143
#> 549 432.938138 0.04806037 0.7092654 1.409909 0.58179973 1.718805 0.90800986
#> 550 433.789890 0.04801316 0.7092834 1.409874 0.58182299 1.718736 0.90809804
#> 551 434.641642 0.04796609 0.7093013 1.409838 0.58184616 1.718667 0.90818595
#> 552 435.493393 0.04791916 0.7093192 1.409803 0.58186925 1.718599 0.90827362
#> 553 436.345145 0.04787237 0.7093370 1.409767 0.58189225 1.718531 0.90836103
#> 554 437.196897 0.04782571 0.7093547 1.409732 0.58191516 1.718464 0.90844819
#> 555 438.048649 0.04777919 0.7093723 1.409697 0.58193798 1.718396 0.90853510
#> 556 438.900400 0.04773281 0.7093899 1.409662 0.58196072 1.718329 0.90862176
#> 557 439.752152 0.04768656 0.7094074 1.409627 0.58198338 1.718262 0.90870818
#> 558 440.603904 0.04764045 0.7094249 1.409593 0.58200594 1.718196 0.90879434
#> 559 441.455656 0.04759447 0.7094422 1.409558 0.58202843 1.718129 0.90888026
#> 560 442.307407 0.04754862 0.7094596 1.409524 0.58205083 1.718063 0.90896594
#> 561 443.159159 0.04750290 0.7094768 1.409489 0.58207314 1.717997 0.90905138
#> 562 444.010911 0.04745732 0.7094940 1.409455 0.58209538 1.717932 0.90913657
#> 563 444.862663 0.04741186 0.7095111 1.409421 0.58211752 1.717866 0.90922152
#> 564 445.100000 0.04739922 0.7095159 1.409412 0.58212368 1.717848 0.90924515
#> 565 445.714414 0.04736654 0.7095282 1.409387 0.58213959 1.717801 0.90930623
#> 566 446.566166 0.04732135 0.7095452 1.409354 0.58216158 1.717736 0.90939071
#> 567 447.417918 0.04727628 0.7095621 1.409320 0.58218348 1.717672 0.90947494
#> 568 448.269670 0.04723135 0.7095790 1.409286 0.58220531 1.717607 0.90955894
#> 569 449.121421 0.04718654 0.7095958 1.409253 0.58222705 1.717543 0.90964271
#> 570 449.790000 0.04715146 0.7096089 1.409227 0.58224406 1.717493 0.90970829
#> 571 449.973173 0.04714186 0.7096125 1.409220 0.58224871 1.717479 0.90972624
#> 572 450.824925 0.04709730 0.7096292 1.409187 0.58227029 1.717415 0.90980954
#> 573 451.676677 0.04705288 0.7096458 1.409154 0.58229180 1.717352 0.90989260
#> 574 452.528428 0.04700857 0.7096624 1.409121 0.58231322 1.717289 0.90997544
#> 575 453.380180 0.04696440 0.7096789 1.409088 0.58233457 1.717226 0.91005804
#> 576 454.231932 0.04692034 0.7096953 1.409055 0.58235584 1.717163 0.91014042
#> 577 455.083684 0.04687641 0.7097117 1.409023 0.58237703 1.717101 0.91022257
#> 578 455.935435 0.04683261 0.7097280 1.408990 0.58239815 1.717038 0.91030449
#> 579 456.787187 0.04678892 0.7097443 1.408958 0.58241919 1.716976 0.91038619
#> 580 457.638939 0.04674536 0.7097605 1.408926 0.58244015 1.716915 0.91046766
#> 581 458.490691 0.04670192 0.7097766 1.408894 0.58246104 1.716853 0.91054891
#> 582 459.342442 0.04665860 0.7097927 1.408862 0.58248185 1.716792 0.91062993
#> 583 460.194194 0.04661540 0.7098088 1.408830 0.58250258 1.716731 0.91071074
#> 584 461.045946 0.04657232 0.7098247 1.408798 0.58252324 1.716670 0.91079132
#> 585 461.897698 0.04652936 0.7098406 1.408767 0.58254383 1.716609 0.91087169
#> 586 462.749449 0.04648652 0.7098565 1.408735 0.58256435 1.716549 0.91095184
#> 587 463.601201 0.04644380 0.7098723 1.408704 0.58258479 1.716488 0.91103177
#> 588 464.452953 0.04640119 0.7098880 1.408673 0.58260515 1.716428 0.91111148
#> 589 465.304705 0.04635870 0.7099037 1.408642 0.58262545 1.716369 0.91119098
#> 590 466.156456 0.04631633 0.7099193 1.408611 0.58264567 1.716309 0.91127026
#> 591 467.008208 0.04627407 0.7099349 1.408580 0.58266582 1.716250 0.91134933
#> 592 467.859960 0.04623193 0.7099504 1.408549 0.58268590 1.716190 0.91142819
#> 593 468.711712 0.04618991 0.7099659 1.408518 0.58270591 1.716132 0.91150683
#> 594 469.563463 0.04614800 0.7099813 1.408488 0.58272585 1.716073 0.91158527
#> 595 470.415215 0.04610620 0.7099967 1.408457 0.58274572 1.716014 0.91166349
#> 596 471.266967 0.04606451 0.7100120 1.408427 0.58276552 1.715956 0.91174151
#> 597 472.118719 0.04602294 0.7100272 1.408397 0.58278524 1.715898 0.91181931
#> 598 472.970470 0.04598148 0.7100424 1.408367 0.58280490 1.715840 0.91189692
#> 599 473.822222 0.04594014 0.7100575 1.408337 0.58282449 1.715782 0.91197431
#> 600 474.673974 0.04589890 0.7100726 1.408307 0.58284402 1.715725 0.91205150
#> 601 475.020000 0.04588218 0.7100787 1.408295 0.58285193 1.715702 0.91208280
#> 602 475.525726 0.04585778 0.7100876 1.408277 0.58286347 1.715668 0.91212849
#> 603 476.377477 0.04581676 0.7101026 1.408247 0.58288286 1.715611 0.91220527
#> 604 477.229229 0.04577586 0.7101175 1.408218 0.58290218 1.715554 0.91228185
#> 605 478.080981 0.04573506 0.7101324 1.408188 0.58292143 1.715497 0.91235823
#> 606 478.932733 0.04569437 0.7101472 1.408159 0.58294061 1.715441 0.91243441
#> 607 479.784484 0.04565380 0.7101620 1.408129 0.58295973 1.715384 0.91251038
#> 608 480.636236 0.04561333 0.7101767 1.408100 0.58297878 1.715328 0.91258616
#> 609 481.487988 0.04557296 0.7101914 1.408071 0.58299777 1.715272 0.91266175
#> 610 482.339740 0.04553271 0.7102060 1.408042 0.58301669 1.715217 0.91273713
#> 611 483.191491 0.04549256 0.7102206 1.408013 0.58303555 1.715161 0.91281232
#> 612 484.043243 0.04545252 0.7102351 1.407984 0.58305434 1.715106 0.91288731
#> 613 484.710000 0.04542124 0.7102464 1.407962 0.58306901 1.715063 0.91294588
#> 614 484.894995 0.04541258 0.7102496 1.407956 0.58307307 1.715051 0.91296211
#> 615 485.746747 0.04537274 0.7102640 1.407927 0.58309173 1.714996 0.91303671
#> 616 486.598498 0.04533302 0.7102784 1.407899 0.58311033 1.714941 0.91311112
#> 617 487.450250 0.04529339 0.7102927 1.407870 0.58312887 1.714887 0.91318534
#> 618 488.302002 0.04525387 0.7103070 1.407842 0.58314735 1.714832 0.91325937
#> 619 489.153754 0.04521446 0.7103212 1.407814 0.58316576 1.714778 0.91333321
#> 620 490.005506 0.04517514 0.7103354 1.407786 0.58318411 1.714724 0.91340686
#> 621 490.857257 0.04513593 0.7103495 1.407758 0.58320239 1.714671 0.91348032
#> 622 491.709009 0.04509682 0.7103636 1.407730 0.58322062 1.714617 0.91355359
#> 623 492.560761 0.04505781 0.7103776 1.407702 0.58323878 1.714564 0.91362667
#> 624 493.412513 0.04501890 0.7103916 1.407674 0.58325688 1.714510 0.91369957
#> 625 494.264264 0.04498010 0.7104055 1.407647 0.58327493 1.714457 0.91377228
#> 626 495.116016 0.04494139 0.7104194 1.407619 0.58329291 1.714405 0.91384481
#> 627 495.967768 0.04490278 0.7104333 1.407592 0.58331083 1.714352 0.91391715
#> 628 496.819520 0.04486428 0.7104471 1.407564 0.58332869 1.714299 0.91398931
#> 629 497.671271 0.04482587 0.7104608 1.407537 0.58334649 1.714247 0.91406129
#> 630 498.523023 0.04478756 0.7104745 1.407510 0.58336423 1.714195 0.91413308
#> 631 499.374775 0.04474935 0.7104882 1.407483 0.58338192 1.714143 0.91420470
#> 632 500.226527 0.04471123 0.7105018 1.407456 0.58339954 1.714091 0.91427613
#> 633 501.078278 0.04467322 0.7105154 1.407429 0.58341711 1.714040 0.91434739
#> 634 501.930030 0.04463530 0.7105289 1.407402 0.58343462 1.713988 0.91441847
#> 635 502.781782 0.04459747 0.7105424 1.407376 0.58345207 1.713937 0.91448937
#> 636 503.633534 0.04455974 0.7105558 1.407349 0.58346946 1.713886 0.91456009
#> 637 504.485285 0.04452211 0.7105692 1.407323 0.58348680 1.713835 0.91463063
#> 638 505.337037 0.04448457 0.7105825 1.407296 0.58350408 1.713784 0.91470100
#> 639 506.188789 0.04444713 0.7105958 1.407270 0.58352130 1.713734 0.91477120
#> 640 507.040541 0.04440978 0.7106091 1.407243 0.58353846 1.713683 0.91484122
#> 641 507.892292 0.04437253 0.7106223 1.407217 0.58355557 1.713633 0.91491106
#> 642 508.744044 0.04433537 0.7106355 1.407191 0.58357263 1.713583 0.91498074
#> 643 509.595796 0.04429830 0.7106486 1.407165 0.58358962 1.713533 0.91505024
#> 644 510.447548 0.04426133 0.7106617 1.407139 0.58360657 1.713483 0.91511957
#> 645 511.299299 0.04422445 0.7106747 1.407113 0.58362345 1.713434 0.91518873
#> 646 512.151051 0.04418766 0.7106877 1.407088 0.58364029 1.713384 0.91525772
#> 647 513.002803 0.04415096 0.7107007 1.407062 0.58365707 1.713335 0.91532654
#> 648 513.854555 0.04411435 0.7107136 1.407037 0.58367379 1.713286 0.91539519
#> 649 514.706306 0.04407784 0.7107265 1.407011 0.58369046 1.713237 0.91546368
#> 650 515.558058 0.04404141 0.7107393 1.406986 0.58370708 1.713188 0.91553199
#> 651 516.409810 0.04400507 0.7107521 1.406960 0.58372364 1.713139 0.91560014
#> 652 517.261562 0.04396883 0.7107649 1.406935 0.58374015 1.713091 0.91566813
#> 653 518.113313 0.04393267 0.7107776 1.406910 0.58375661 1.713043 0.91573595
#> 654 518.965065 0.04389661 0.7107902 1.406885 0.58377301 1.712995 0.91580360
#> 655 519.816817 0.04386063 0.7108029 1.406860 0.58378936 1.712947 0.91587109
#> 656 520.668569 0.04382474 0.7108154 1.406835 0.58380566 1.712899 0.91593842
#> 657 521.520320 0.04378893 0.7108280 1.406810 0.58382191 1.712851 0.91600559
#> 658 522.372072 0.04375322 0.7108405 1.406785 0.58383810 1.712804 0.91607259
#> 659 523.223824 0.04371759 0.7108530 1.406761 0.58385425 1.712756 0.91613943
#> 660 523.700000 0.04369771 0.7108599 1.406747 0.58386325 1.712730 0.91617673
#> 661 524.075576 0.04368205 0.7108654 1.406736 0.58387034 1.712709 0.91620611
#> 662 524.927327 0.04364660 0.7108778 1.406712 0.58388638 1.712662 0.91627263
#> 663 525.779079 0.04361123 0.7108901 1.406687 0.58390237 1.712615 0.91633900
#> 664 526.630831 0.04357595 0.7109024 1.406663 0.58391832 1.712568 0.91640520
#> 665 527.482583 0.04354075 0.7109147 1.406639 0.58393421 1.712522 0.91647125
#> 666 528.334334 0.04350564 0.7109269 1.406614 0.58395005 1.712475 0.91653713
#> 667 529.186086 0.04347062 0.7109391 1.406590 0.58396584 1.712429 0.91660287
#> 668 530.037838 0.04343567 0.7109513 1.406566 0.58398158 1.712383 0.91666844
#> 669 530.889590 0.04340082 0.7109634 1.406542 0.58399727 1.712337 0.91673386
#> 670 531.741341 0.04336604 0.7109755 1.406518 0.58401291 1.712291 0.91679913
#> 671 532.593093 0.04333135 0.7109875 1.406494 0.58402851 1.712245 0.91686424
#> 672 533.444845 0.04329674 0.7109995 1.406471 0.58404405 1.712200 0.91692919
#> 673 534.296597 0.04326222 0.7110115 1.406447 0.58405955 1.712154 0.91699400
#> 674 535.148348 0.04322778 0.7110234 1.406423 0.58407500 1.712109 0.91705865
#> 675 536.000100 0.04319342 0.7110353 1.406400 0.58409040 1.712064 0.91712315
#> 676 536.851852 0.04315914 0.7110472 1.406376 0.58410575 1.712019 0.91718750
#> 677 537.703604 0.04312494 0.7110590 1.406353 0.58412106 1.711974 0.91725169
#> 678 538.555355 0.04309083 0.7110708 1.406330 0.58413632 1.711929 0.91731574
#> 679 539.407107 0.04305679 0.7110825 1.406307 0.58415153 1.711885 0.91737964
#> 680 540.258859 0.04302284 0.7110942 1.406283 0.58416670 1.711840 0.91744339
#> 681 541.110611 0.04298896 0.7111059 1.406260 0.58418181 1.711796 0.91750699
#> 682 541.962362 0.04295517 0.7111175 1.406237 0.58419688 1.711752 0.91757044
#> 683 542.814114 0.04292145 0.7111291 1.406214 0.58421191 1.711708 0.91763375
#> 684 543.665866 0.04288782 0.7111407 1.406192 0.58422689 1.711664 0.91769691
#> 685 544.517618 0.04285426 0.7111522 1.406169 0.58424182 1.711620 0.91775992
#> 686 545.369369 0.04282079 0.7111637 1.406146 0.58425671 1.711576 0.91782279
#> 687 546.221121 0.04278739 0.7111752 1.406123 0.58427155 1.711533 0.91788551
#> 688 547.072873 0.04275406 0.7111866 1.406101 0.58428635 1.711490 0.91794809
#> 689 547.924625 0.04272082 0.7111980 1.406078 0.58430110 1.711446 0.91801052
#> 690 548.776376 0.04268765 0.7112093 1.406056 0.58431581 1.711403 0.91807282
#> 691 549.628128 0.04265457 0.7112207 1.406033 0.58433048 1.711360 0.91813496
#> 692 550.479880 0.04262155 0.7112319 1.406011 0.58434510 1.711318 0.91819697
#> 693 551.331632 0.04258862 0.7112432 1.405989 0.58435967 1.711275 0.91825883
#> 694 552.183383 0.04255576 0.7112544 1.405967 0.58437420 1.711232 0.91832056
#> 695 553.035135 0.04252297 0.7112656 1.405945 0.58438869 1.711190 0.91838214
#> 696 553.886887 0.04249027 0.7112767 1.405923 0.58440313 1.711148 0.91844358
#> 697 554.380000 0.04247137 0.7112832 1.405910 0.58441147 1.711123 0.91847909
#> 698 554.738639 0.04245763 0.7112879 1.405901 0.58441753 1.711105 0.91850489
#> 699 555.590390 0.04242508 0.7112989 1.405879 0.58443189 1.711063 0.91856605
#> 700 556.442142 0.04239259 0.7113100 1.405857 0.58444620 1.711021 0.91862708
#> 701 557.293894 0.04236019 0.7113210 1.405835 0.58446048 1.710980 0.91868797
#> 702 558.145646 0.04232785 0.7113320 1.405813 0.58447471 1.710938 0.91874872
#> 703 558.997397 0.04229559 0.7113429 1.405792 0.58448889 1.710897 0.91880933
#> 704 559.849149 0.04226341 0.7113539 1.405770 0.58450304 1.710855 0.91886981
#> 705 560.700901 0.04223129 0.7113647 1.405749 0.58451714 1.710814 0.91893015
#> 706 561.552653 0.04219925 0.7113756 1.405727 0.58453120 1.710773 0.91899035
#> 707 562.404404 0.04216729 0.7113864 1.405706 0.58454522 1.710732 0.91905043
#> 708 563.256156 0.04213539 0.7113972 1.405684 0.58455920 1.710691 0.91911036
#> 709 564.107908 0.04210357 0.7114080 1.405663 0.58457313 1.710650 0.91917017
#> 710 564.959660 0.04207182 0.7114187 1.405642 0.58458703 1.710609 0.91922984
#> 711 565.811411 0.04204014 0.7114294 1.405621 0.58460088 1.710569 0.91928937
#> 712 566.663163 0.04200853 0.7114400 1.405600 0.58461470 1.710528 0.91934878
#> 713 567.514915 0.04197700 0.7114507 1.405579 0.58462847 1.710488 0.91940805
#> 714 568.366667 0.04194553 0.7114613 1.405558 0.58464220 1.710448 0.91946719
#> 715 569.218418 0.04191414 0.7114718 1.405537 0.58465589 1.710408 0.91952620
#> 716 570.070170 0.04188281 0.7114824 1.405516 0.58466955 1.710368 0.91958508
#> 717 570.921922 0.04185156 0.7114929 1.405495 0.58468316 1.710328 0.91964383
#> 718 571.773674 0.04182037 0.7115034 1.405475 0.58469673 1.710288 0.91970245
#> 719 572.625425 0.04178926 0.7115138 1.405454 0.58471027 1.710249 0.91976094
#> 720 573.477177 0.04175822 0.7115242 1.405434 0.58472376 1.710209 0.91981931
#> 721 574.328929 0.04172724 0.7115346 1.405413 0.58473722 1.710170 0.91987754
#> 722 575.180681 0.04169633 0.7115450 1.405393 0.58475063 1.710131 0.91993565
#> 723 576.032432 0.04166549 0.7115553 1.405372 0.58476401 1.710092 0.91999363
#> 724 576.884184 0.04163472 0.7115656 1.405352 0.58477735 1.710053 0.92005149
#> 725 577.735936 0.04160402 0.7115758 1.405332 0.58479065 1.710014 0.92010921
#> 726 578.587688 0.04157339 0.7115861 1.405311 0.58480391 1.709975 0.92016682
#> 727 579.439439 0.04154282 0.7115963 1.405291 0.58481713 1.709936 0.92022429
#> 728 580.291191 0.04151232 0.7116065 1.405271 0.58483032 1.709898 0.92028164
#> 729 581.142943 0.04148189 0.7116166 1.405251 0.58484347 1.709859 0.92033887
#> 730 581.994695 0.04145152 0.7116267 1.405231 0.58485658 1.709821 0.92039598
#> 731 582.846446 0.04142122 0.7116368 1.405211 0.58486965 1.709783 0.92045296
#> 732 583.698198 0.04139099 0.7116469 1.405191 0.58488269 1.709745 0.92050981
#> 733 584.549950 0.04136082 0.7116569 1.405172 0.58489569 1.709707 0.92056655
#> 734 585.401702 0.04133072 0.7116669 1.405152 0.58490865 1.709669 0.92062316
#> 735 586.253453 0.04130069 0.7116769 1.405132 0.58492157 1.709631 0.92067965
#> 736 587.105205 0.04127072 0.7116868 1.405112 0.58493446 1.709593 0.92073602
#> 737 587.956957 0.04124081 0.7116967 1.405093 0.58494731 1.709556 0.92079227
#> 738 588.808709 0.04121097 0.7117066 1.405073 0.58496013 1.709518 0.92084840
#> 739 589.660460 0.04118120 0.7117165 1.405054 0.58497291 1.709481 0.92090441
#> 740 590.512212 0.04115149 0.7117263 1.405034 0.58498565 1.709444 0.92096030
#> 741 591.363964 0.04112184 0.7117361 1.405015 0.58499836 1.709407 0.92101607
#> 742 592.215716 0.04109226 0.7117459 1.404996 0.58501103 1.709369 0.92107172
#> 743 593.067467 0.04106274 0.7117557 1.404977 0.58502366 1.709333 0.92112725
#> 744 593.919219 0.04103329 0.7117654 1.404957 0.58503626 1.709296 0.92118267
#> 745 594.770971 0.04100390 0.7117751 1.404938 0.58504883 1.709259 0.92123797
#> 746 595.622723 0.04097457 0.7117847 1.404919 0.58506136 1.709222 0.92129315
#> 747 596.474474 0.04094530 0.7117944 1.404900 0.58507385 1.709186 0.92134821
#> 748 597.326226 0.04091610 0.7118040 1.404881 0.58508631 1.709150 0.92140316
#> 749 598.177978 0.04088696 0.7118136 1.404862 0.58509874 1.709113 0.92145799
#> 750 599.029730 0.04085788 0.7118231 1.404843 0.58511113 1.709077 0.92151271
#> 751 599.881481 0.04082886 0.7118327 1.404825 0.58512348 1.709041 0.92156731
#> 752 600.733233 0.04079991 0.7118422 1.404806 0.58513580 1.709005 0.92162180
#> 753 601.584985 0.04077101 0.7118517 1.404787 0.58514809 1.708969 0.92167617
#> 754 602.436737 0.04074218 0.7118611 1.404768 0.58516035 1.708933 0.92173043
#> 755 603.288488 0.04071341 0.7118706 1.404750 0.58517256 1.708898 0.92178458
#> 756 604.140240 0.04068470 0.7118800 1.404731 0.58518475 1.708862 0.92183861
#> 757 604.991992 0.04065605 0.7118893 1.404713 0.58519690 1.708827 0.92189253
#> 758 605.843744 0.04062746 0.7118987 1.404694 0.58520902 1.708791 0.92194634
#> 759 606.695495 0.04059893 0.7119080 1.404676 0.58522111 1.708756 0.92200004
#> 760 607.547247 0.04057046 0.7119173 1.404658 0.58523316 1.708721 0.92205363
#> 761 608.398999 0.04054205 0.7119266 1.404639 0.58524518 1.708686 0.92210710
#> 762 609.250751 0.04051371 0.7119358 1.404621 0.58525717 1.708651 0.92216046
#> 763 610.102503 0.04048542 0.7119450 1.404603 0.58526912 1.708616 0.92221372
#> 764 610.954254 0.04045718 0.7119542 1.404585 0.58528104 1.708581 0.92226686
#> 765 611.806006 0.04042901 0.7119634 1.404567 0.58529293 1.708546 0.92231990
#> 766 612.657758 0.04040090 0.7119726 1.404549 0.58530479 1.708512 0.92237282
#> 767 612.980000 0.04039028 0.7119760 1.404542 0.58530926 1.708499 0.92239282
#> 768 613.509510 0.04037284 0.7119817 1.404531 0.58531661 1.708477 0.92242564
#> 769 614.361261 0.04034485 0.7119908 1.404513 0.58532840 1.708443 0.92247835
#> 770 615.213013 0.04031691 0.7119999 1.404495 0.58534016 1.708408 0.92253095
#> 771 616.064765 0.04028903 0.7120089 1.404477 0.58535189 1.708374 0.92258344
#> 772 616.740000 0.04026697 0.7120161 1.404463 0.58536116 1.708347 0.92262498
#> 773 616.916517 0.04026121 0.7120179 1.404459 0.58536358 1.708340 0.92263582
#> 774 617.768268 0.04023344 0.7120269 1.404441 0.58537525 1.708306 0.92268810
#> 775 618.620020 0.04020574 0.7120359 1.404424 0.58538688 1.708272 0.92274027
#> 776 619.260000 0.04018495 0.7120426 1.404410 0.58539560 1.708247 0.92277940
#> 777 619.471772 0.04017809 0.7120449 1.404406 0.58539848 1.708238 0.92279234
#> 778 620.323524 0.04015049 0.7120538 1.404388 0.58541006 1.708204 0.92284430
#> 779 621.175275 0.04012296 0.7120627 1.404371 0.58542160 1.708171 0.92289615
#> 780 622.027027 0.04009548 0.7120716 1.404353 0.58543310 1.708137 0.92294790
#> 781 622.878779 0.04006805 0.7120804 1.404336 0.58544458 1.708104 0.92299955
#> 782 623.730531 0.04004069 0.7120892 1.404318 0.58545603 1.708070 0.92305109
#> 783 624.582282 0.04001337 0.7120981 1.404301 0.58546745 1.708037 0.92310253
#> 784 625.434034 0.03998612 0.7121068 1.404284 0.58547883 1.708004 0.92315386
#> 785 626.130000 0.03996389 0.7121140 1.404270 0.58548811 1.707977 0.92319573
#> 786 626.285786 0.03995892 0.7121156 1.404266 0.58549019 1.707971 0.92320509
#> 787 627.137538 0.03993177 0.7121243 1.404249 0.58550151 1.707938 0.92325621
#> 788 627.989289 0.03990468 0.7121330 1.404232 0.58551281 1.707905 0.92330724
#> 789 628.841041 0.03987765 0.7121417 1.404215 0.58552407 1.707872 0.92335816
#> 790 629.692793 0.03985067 0.7121504 1.404198 0.58553531 1.707839 0.92340898
#> 791 630.544545 0.03982375 0.7121590 1.404181 0.58554652 1.707806 0.92345970
#> 792 631.396296 0.03979688 0.7121677 1.404164 0.58555769 1.707774 0.92351031
#> 793 632.248048 0.03977006 0.7121763 1.404147 0.58556884 1.707741 0.92356083
#> 794 633.099800 0.03974330 0.7121848 1.404130 0.58557996 1.707709 0.92361124
#> 795 633.951552 0.03971659 0.7121934 1.404113 0.58559104 1.707676 0.92366156
#> 796 634.803303 0.03968994 0.7122019 1.404096 0.58560210 1.707644 0.92371177
#> 797 635.655055 0.03966334 0.7122104 1.404079 0.58561313 1.707612 0.92376189
#> 798 636.506807 0.03963679 0.7122189 1.404063 0.58562413 1.707580 0.92381190
#> 799 637.358559 0.03961030 0.7122274 1.404046 0.58563511 1.707548 0.92386182
#> 800 638.210310 0.03958386 0.7122358 1.404029 0.58564605 1.707516 0.92391164
#> 801 639.062062 0.03955747 0.7122442 1.404013 0.58565696 1.707484 0.92396136
#> 802 639.913814 0.03953113 0.7122526 1.403996 0.58566785 1.707452 0.92401098
#> 803 640.765566 0.03950485 0.7122610 1.403980 0.58567871 1.707421 0.92406051
#> 804 641.617317 0.03947862 0.7122694 1.403963 0.58568954 1.707389 0.92410993
#> 805 642.469069 0.03945244 0.7122777 1.403947 0.58570034 1.707358 0.92415927
#> 806 643.320821 0.03942632 0.7122860 1.403930 0.58571111 1.707326 0.92420850
#> 807 644.172573 0.03940024 0.7122943 1.403914 0.58572186 1.707295 0.92425764
#> 808 645.024324 0.03937422 0.7123026 1.403898 0.58573258 1.707264 0.92430668
#> 809 645.876076 0.03934825 0.7123108 1.403882 0.58574327 1.707233 0.92435562
#> 810 646.727828 0.03932233 0.7123190 1.403865 0.58575393 1.707202 0.92440447
#> 811 647.579580 0.03929646 0.7123272 1.403849 0.58576457 1.707171 0.92445323
#> 812 648.431331 0.03927064 0.7123354 1.403833 0.58577517 1.707140 0.92450189
#> 813 649.283083 0.03924488 0.7123436 1.403817 0.58578575 1.707109 0.92455045
#> 814 650.134835 0.03921916 0.7123517 1.403801 0.58579631 1.707078 0.92459893
#> 815 650.986587 0.03919349 0.7123598 1.403785 0.58580683 1.707047 0.92464730
#> 816 651.838338 0.03916788 0.7123679 1.403769 0.58581733 1.707017 0.92469559
#> 817 652.690090 0.03914231 0.7123760 1.403753 0.58582780 1.706986 0.92474378
#> 818 653.541842 0.03911680 0.7123841 1.403737 0.58583825 1.706956 0.92479188
#> 819 654.393594 0.03909133 0.7123921 1.403721 0.58584867 1.706925 0.92483988
#> 820 655.245345 0.03906592 0.7124001 1.403706 0.58585906 1.706895 0.92488779
#> 821 656.097097 0.03904055 0.7124081 1.403690 0.58586943 1.706865 0.92493561
#> 822 656.948849 0.03901523 0.7124161 1.403674 0.58587977 1.706835 0.92498334
#> 823 657.800601 0.03898997 0.7124240 1.403658 0.58589008 1.706805 0.92503098
#> 824 658.652352 0.03896475 0.7124320 1.403643 0.58590037 1.706775 0.92507853
#> 825 659.504104 0.03893958 0.7124399 1.403627 0.58591063 1.706745 0.92512598
#> 826 660.355856 0.03891446 0.7124478 1.403612 0.58592086 1.706715 0.92517335
#> 827 661.207608 0.03888939 0.7124557 1.403596 0.58593107 1.706685 0.92522062
#> 828 662.059359 0.03886436 0.7124635 1.403581 0.58594126 1.706656 0.92526780
#> 829 662.911111 0.03883939 0.7124713 1.403565 0.58595141 1.706626 0.92531490
#> 830 663.762863 0.03881446 0.7124792 1.403550 0.58596155 1.706597 0.92536190
#> 831 664.614615 0.03878958 0.7124869 1.403534 0.58597165 1.706567 0.92540882
#> 832 665.466366 0.03876475 0.7124947 1.403519 0.58598173 1.706538 0.92545565
#> 833 666.318118 0.03873996 0.7125025 1.403504 0.58599179 1.706509 0.92550238
#> 834 667.169870 0.03871522 0.7125102 1.403489 0.58600182 1.706479 0.92554903
#> 835 668.021622 0.03869054 0.7125179 1.403473 0.58601183 1.706450 0.92559560
#> 836 668.873373 0.03866589 0.7125256 1.403458 0.58602181 1.706421 0.92564207
#> 837 669.725125 0.03864130 0.7125333 1.403443 0.58603176 1.706392 0.92568846
#> 838 670.576877 0.03861675 0.7125410 1.403428 0.58604170 1.706363 0.92573476
#> 839 671.428629 0.03859225 0.7125486 1.403413 0.58605160 1.706334 0.92578097
#> 840 672.280380 0.03856779 0.7125562 1.403398 0.58606148 1.706306 0.92582709
#> 841 673.132132 0.03854338 0.7125638 1.403383 0.58607134 1.706277 0.92587313
#> 842 673.983884 0.03851902 0.7125714 1.403368 0.58608117 1.706248 0.92591909
#> 843 674.835636 0.03849471 0.7125790 1.403353 0.58609098 1.706220 0.92596495
#> 844 675.687387 0.03847043 0.7125865 1.403338 0.58610077 1.706191 0.92601073
#> 845 676.539139 0.03844621 0.7125940 1.403324 0.58611053 1.706163 0.92605643
#> 846 677.390891 0.03842203 0.7126015 1.403309 0.58612026 1.706134 0.92610204
#> 847 678.242643 0.03839790 0.7126090 1.403294 0.58612997 1.706106 0.92614757
#> 848 679.094394 0.03837381 0.7126165 1.403279 0.58613966 1.706078 0.92619301
#> 849 679.946146 0.03834977 0.7126240 1.403265 0.58614933 1.706050 0.92623837
#> 850 680.797898 0.03832577 0.7126314 1.403250 0.58615897 1.706022 0.92628364
#> 851 681.649650 0.03830182 0.7126388 1.403235 0.58616858 1.705994 0.92632883
#> 852 682.501401 0.03827791 0.7126462 1.403221 0.58617818 1.705966 0.92637394
#> 853 683.353153 0.03825405 0.7126536 1.403206 0.58618775 1.705938 0.92641896
#> 854 684.204905 0.03823023 0.7126609 1.403192 0.58619729 1.705910 0.92646390
#> 855 685.056657 0.03820646 0.7126683 1.403177 0.58620682 1.705883 0.92650876
#> 856 685.590000 0.03819159 0.7126729 1.403168 0.58621277 1.705865 0.92653680
#> 857 685.908408 0.03818273 0.7126756 1.403163 0.58621632 1.705855 0.92655353
#> 858 686.760160 0.03815904 0.7126829 1.403149 0.58622579 1.705827 0.92659822
#> 859 687.611912 0.03813540 0.7126902 1.403134 0.58623525 1.705800 0.92664283
#> 860 688.463664 0.03811180 0.7126975 1.403120 0.58624468 1.705772 0.92668736
#> 861 689.315415 0.03808825 0.7127047 1.403106 0.58625409 1.705745 0.92673181
#> 862 690.167167 0.03806474 0.7127120 1.403091 0.58626347 1.705718 0.92677617
#> 863 691.018919 0.03804127 0.7127192 1.403077 0.58627283 1.705690 0.92682046
#> 864 691.870671 0.03801785 0.7127264 1.403063 0.58628217 1.705663 0.92686466
#> 865 692.722422 0.03799447 0.7127336 1.403049 0.58629149 1.705636 0.92690879
#> 866 693.574174 0.03797113 0.7127407 1.403035 0.58630079 1.705609 0.92695283
#> 867 694.425926 0.03794784 0.7127479 1.403021 0.58631006 1.705582 0.92699679
#> 868 695.277678 0.03792459 0.7127550 1.403007 0.58631931 1.705555 0.92704068
#> 869 696.129429 0.03790138 0.7127621 1.402993 0.58632854 1.705528 0.92708448
#> 870 696.981181 0.03787821 0.7127692 1.402979 0.58633774 1.705502 0.92712821
#> 871 697.832933 0.03785509 0.7127763 1.402965 0.58634693 1.705475 0.92717185
#> 872 698.684685 0.03783201 0.7127834 1.402951 0.58635609 1.705448 0.92721542
#> 873 699.536436 0.03780897 0.7127904 1.402937 0.58636523 1.705422 0.92725891
#> 874 700.388188 0.03778597 0.7127975 1.402923 0.58637435 1.705395 0.92730232
#> 875 701.239940 0.03776302 0.7128045 1.402909 0.58638344 1.705369 0.92734565
#> 876 702.091692 0.03774010 0.7128115 1.402895 0.58639252 1.705342 0.92738890
#> 877 702.943443 0.03771723 0.7128185 1.402882 0.58640157 1.705316 0.92743208
#> 878 703.795195 0.03769440 0.7128254 1.402868 0.58641060 1.705290 0.92747518
#> 879 704.646947 0.03767161 0.7128324 1.402854 0.58641961 1.705264 0.92751820
#> 880 705.498699 0.03764887 0.7128393 1.402841 0.58642860 1.705237 0.92756115
#> 881 706.350450 0.03762616 0.7128462 1.402827 0.58643757 1.705211 0.92760402
#> 882 707.202202 0.03760349 0.7128531 1.402814 0.58644652 1.705185 0.92764681
#> 883 708.053954 0.03758087 0.7128600 1.402800 0.58645544 1.705159 0.92768952
#> 884 708.905706 0.03755829 0.7128668 1.402787 0.58646435 1.705133 0.92773216
#> 885 709.757457 0.03753574 0.7128737 1.402773 0.58647323 1.705108 0.92777473
#> 886 710.609209 0.03751324 0.7128805 1.402760 0.58648209 1.705082 0.92781721
#> 887 711.460961 0.03749078 0.7128873 1.402746 0.58649093 1.705056 0.92785963
#> 888 712.312713 0.03746836 0.7128941 1.402733 0.58649975 1.705031 0.92790196
#> 889 713.164464 0.03744598 0.7129009 1.402719 0.58650855 1.705005 0.92794423
#> 890 714.016216 0.03742363 0.7129077 1.402706 0.58651733 1.704979 0.92798642
#> 891 714.867968 0.03740133 0.7129144 1.402693 0.58652609 1.704954 0.92802853
#> 892 715.719720 0.03737907 0.7129212 1.402680 0.58653483 1.704929 0.92807057
#> 893 716.571471 0.03735685 0.7129279 1.402666 0.58654355 1.704903 0.92811253
#> 894 717.423223 0.03733467 0.7129346 1.402653 0.58655224 1.704878 0.92815443
#> 895 718.274975 0.03731252 0.7129413 1.402640 0.58656092 1.704853 0.92819624
#> 896 719.126727 0.03729042 0.7129480 1.402627 0.58656958 1.704828 0.92823799
#> 897 719.978478 0.03726836 0.7129546 1.402614 0.58657822 1.704802 0.92827966
#> 898 720.830230 0.03724633 0.7129613 1.402601 0.58658683 1.704777 0.92832126
#> 899 721.681982 0.03722435 0.7129679 1.402588 0.58659543 1.704752 0.92836278
#> 900 722.533734 0.03720240 0.7129745 1.402575 0.58660401 1.704728 0.92840424
#> 901 723.385485 0.03718049 0.7129811 1.402562 0.58661256 1.704703 0.92844562
#> 902 724.237237 0.03715862 0.7129877 1.402549 0.58662110 1.704678 0.92848693
#> 903 725.088989 0.03713679 0.7129943 1.402536 0.58662962 1.704653 0.92852816
#> 904 725.940741 0.03711500 0.7130008 1.402523 0.58663812 1.704628 0.92856933
#> 905 726.792492 0.03709324 0.7130073 1.402510 0.58664660 1.704604 0.92861042
#> 906 727.644244 0.03707152 0.7130139 1.402497 0.58665506 1.704579 0.92865145
#> 907 728.495996 0.03704985 0.7130204 1.402484 0.58666350 1.704555 0.92869240
#> 908 729.347748 0.03702821 0.7130269 1.402472 0.58667192 1.704530 0.92873328
#> 909 730.199499 0.03700660 0.7130333 1.402459 0.58668032 1.704506 0.92877409
#> 910 731.051251 0.03698504 0.7130398 1.402446 0.58668870 1.704481 0.92881483
#> 911 731.903003 0.03696351 0.7130462 1.402434 0.58669706 1.704457 0.92885550
#> 912 732.754755 0.03694202 0.7130527 1.402421 0.58670540 1.704433 0.92889610
#> 913 733.606507 0.03692057 0.7130591 1.402408 0.58671373 1.704409 0.92893663
#> 914 734.458258 0.03689916 0.7130655 1.402396 0.58672203 1.704385 0.92897709
#> 915 735.310010 0.03687778 0.7130719 1.402383 0.58673032 1.704361 0.92901748
#> 916 736.161762 0.03685644 0.7130783 1.402371 0.58673859 1.704337 0.92905780
#> 917 737.013514 0.03683514 0.7130846 1.402358 0.58674684 1.704313 0.92909805
#> 918 737.865265 0.03681387 0.7130910 1.402346 0.58675507 1.704289 0.92913823
#> 919 738.717017 0.03679264 0.7130973 1.402333 0.58676328 1.704265 0.92917835
#> 920 739.568769 0.03677145 0.7131036 1.402321 0.58677147 1.704241 0.92921839
#> 921 740.420521 0.03675029 0.7131099 1.402308 0.58677965 1.704217 0.92925837
#> 922 741.272272 0.03672917 0.7131162 1.402296 0.58678780 1.704194 0.92929828
#> 923 742.124024 0.03670809 0.7131225 1.402284 0.58679594 1.704170 0.92933812
#> 924 742.975776 0.03668704 0.7131287 1.402271 0.58680406 1.704146 0.92937790
#> 925 743.827528 0.03666603 0.7131350 1.402259 0.58681216 1.704123 0.92941761
#> 926 744.679279 0.03664505 0.7131412 1.402247 0.58682024 1.704099 0.92945724
#> 927 745.531031 0.03662411 0.7131474 1.402235 0.58682831 1.704076 0.92949682
#> 928 746.382783 0.03660321 0.7131536 1.402222 0.58683636 1.704053 0.92953632
#> 929 747.234535 0.03658234 0.7131598 1.402210 0.58684438 1.704029 0.92957576
#> 930 748.086286 0.03656151 0.7131660 1.402198 0.58685239 1.704006 0.92961513
#> 931 748.938038 0.03654072 0.7131721 1.402186 0.58686039 1.703983 0.92965444
#> 932 749.789790 0.03651996 0.7131783 1.402174 0.58686836 1.703960 0.92969368
#> 933 750.641542 0.03649923 0.7131844 1.402162 0.58687632 1.703937 0.92973285
#> 934 751.493293 0.03647854 0.7131905 1.402150 0.58688426 1.703913 0.92977196
#> 935 752.345045 0.03645788 0.7131966 1.402138 0.58689218 1.703890 0.92981100
#> 936 753.196797 0.03643726 0.7132027 1.402126 0.58690008 1.703868 0.92984998
#> 937 754.048549 0.03641668 0.7132088 1.402114 0.58690797 1.703845 0.92988889
#> 938 754.900300 0.03639613 0.7132149 1.402102 0.58691584 1.703822 0.92992774
#> 939 755.752052 0.03637561 0.7132209 1.402090 0.58692369 1.703799 0.92996652
#> 940 756.603804 0.03635513 0.7132270 1.402078 0.58693153 1.703776 0.93000524
#> 941 757.455556 0.03633469 0.7132330 1.402066 0.58693934 1.703754 0.93004389
#> 942 758.307307 0.03631428 0.7132390 1.402055 0.58694714 1.703731 0.93008248
#> 943 759.159059 0.03629390 0.7132450 1.402043 0.58695492 1.703708 0.93012100
#> 944 760.010811 0.03627355 0.7132510 1.402031 0.58696269 1.703686 0.93015946
#> 945 760.862563 0.03625325 0.7132570 1.402019 0.58697044 1.703663 0.93019786
#> 946 761.714314 0.03623297 0.7132629 1.402008 0.58697817 1.703641 0.93023619
#> 947 762.566066 0.03621273 0.7132689 1.401996 0.58698588 1.703618 0.93027446
#> 948 763.417818 0.03619252 0.7132748 1.401984 0.58699358 1.703596 0.93031267
#> 949 763.720000 0.03618536 0.7132769 1.401980 0.58699631 1.703588 0.93032621
#> 950 764.269570 0.03617235 0.7132807 1.401973 0.58700126 1.703574 0.93035081
#> 951 765.121321 0.03615221 0.7132866 1.401961 0.58700892 1.703552 0.93038889
#> 952 765.973073 0.03613210 0.7132925 1.401949 0.58701657 1.703529 0.93042691
#> 953 766.824825 0.03611203 0.7132984 1.401938 0.58702420 1.703507 0.93046486
#> 954 767.676577 0.03609199 0.7133043 1.401926 0.58703181 1.703485 0.93050275
#> 955 768.528328 0.03607199 0.7133101 1.401915 0.58703941 1.703463 0.93054058
#> 956 769.380080 0.03605201 0.7133160 1.401903 0.58704699 1.703441 0.93057835
#> 957 770.231832 0.03603207 0.7133218 1.401892 0.58705455 1.703419 0.93061606
#> 958 771.083584 0.03601217 0.7133276 1.401880 0.58706210 1.703397 0.93065370
#> 959 771.935335 0.03599229 0.7133334 1.401869 0.58706963 1.703375 0.93069128
#> 960 772.787087 0.03597245 0.7133392 1.401858 0.58707715 1.703354 0.93072881
#> 961 773.638839 0.03595265 0.7133450 1.401846 0.58708465 1.703332 0.93076627
#> 962 774.490591 0.03593287 0.7133507 1.401835 0.58709213 1.703310 0.93080366
#> 963 775.342342 0.03591313 0.7133565 1.401824 0.58709959 1.703289 0.93084100
#> 964 776.194094 0.03589342 0.7133622 1.401812 0.58710704 1.703267 0.93087828
#> 965 777.045846 0.03587374 0.7133680 1.401801 0.58711448 1.703245 0.93091550
#> 966 777.897598 0.03585410 0.7133737 1.401790 0.58712190 1.703224 0.93095265
#> 967 778.749349 0.03583448 0.7133794 1.401779 0.58712930 1.703202 0.93098975
#> 968 779.601101 0.03581490 0.7133851 1.401767 0.58713668 1.703181 0.93102679
#> 969 780.452853 0.03579535 0.7133908 1.401756 0.58714405 1.703160 0.93106376
#> 970 781.304605 0.03577584 0.7133964 1.401745 0.58715141 1.703138 0.93110068
#> 971 782.156356 0.03575635 0.7134021 1.401734 0.58715875 1.703117 0.93113754
#> 972 783.008108 0.03573690 0.7134077 1.401723 0.58716607 1.703096 0.93117433
#> 973 783.859860 0.03571748 0.7134134 1.401712 0.58717338 1.703074 0.93121107
#> 974 784.711612 0.03569809 0.7134190 1.401701 0.58718067 1.703053 0.93124775
#> 975 785.563363 0.03567873 0.7134246 1.401690 0.58718795 1.703032 0.93128437
#> 976 786.415115 0.03565940 0.7134302 1.401679 0.58719521 1.703011 0.93132093
#> 977 787.266867 0.03564011 0.7134358 1.401668 0.58720245 1.702990 0.93135743
#> 978 788.118619 0.03562084 0.7134413 1.401657 0.58720968 1.702969 0.93139388
#> 979 788.970370 0.03560161 0.7134469 1.401646 0.58721689 1.702948 0.93143026
#> 980 789.822122 0.03558241 0.7134524 1.401635 0.58722409 1.702927 0.93146659
#> 981 790.673874 0.03556324 0.7134580 1.401624 0.58723128 1.702907 0.93150286
#> 982 791.525626 0.03554410 0.7134635 1.401613 0.58723845 1.702886 0.93153907
#> 983 792.377377 0.03552499 0.7134690 1.401603 0.58724560 1.702865 0.93157523
#> 984 793.229129 0.03550591 0.7134745 1.401592 0.58725274 1.702844 0.93161133
#> 985 794.080881 0.03548686 0.7134800 1.401581 0.58725986 1.702824 0.93164736
#> 986 794.932633 0.03546785 0.7134855 1.401570 0.58726697 1.702803 0.93168335
#> 987 795.784384 0.03544886 0.7134909 1.401559 0.58727406 1.702783 0.93171927
#> 988 796.636136 0.03542991 0.7134964 1.401549 0.58728114 1.702762 0.93175514
#> 989 797.487888 0.03541098 0.7135018 1.401538 0.58728820 1.702742 0.93179095
#> 990 798.339640 0.03539209 0.7135073 1.401527 0.58729525 1.702721 0.93182671
#> 991 799.191391 0.03537322 0.7135127 1.401517 0.58730229 1.702701 0.93186240
#> 992 800.043143 0.03535439 0.7135181 1.401506 0.58730931 1.702680 0.93189805
#> 993 800.894895 0.03533558 0.7135235 1.401496 0.58731631 1.702660 0.93193363
#> 994 801.746647 0.03531681 0.7135289 1.401485 0.58732330 1.702640 0.93196916
#> 995 802.598398 0.03529806 0.7135343 1.401474 0.58733028 1.702620 0.93200463
#> 996 803.450150 0.03527935 0.7135396 1.401464 0.58733724 1.702599 0.93204005
#> 997 804.301902 0.03526066 0.7135450 1.401453 0.58734418 1.702579 0.93207541
#> 998 805.153654 0.03524201 0.7135503 1.401443 0.58735111 1.702559 0.93211072
#> 999 806.005405 0.03522338 0.7135556 1.401432 0.58735803 1.702539 0.93214597
#> 1000 806.857157 0.03520478 0.7135610 1.401422 0.58736493 1.702519 0.93218117
#> 1001 807.708909 0.03518622 0.7135663 1.401412 0.58737182 1.702499 0.93221631
#> 1002 808.560661 0.03516768 0.7135716 1.401401 0.58737870 1.702479 0.93225140
#> 1003 809.412412 0.03514917 0.7135768 1.401391 0.58738556 1.702459 0.93228643
#> 1004 810.264164 0.03513069 0.7135821 1.401380 0.58739240 1.702439 0.93232141
#> 1005 811.115916 0.03511224 0.7135874 1.401370 0.58739923 1.702420 0.93235633
#> 1006 811.967668 0.03509382 0.7135926 1.401360 0.58740605 1.702400 0.93239120
#> 1007 812.819419 0.03507543 0.7135979 1.401349 0.58741286 1.702380 0.93242601
#> 1008 813.671171 0.03505706 0.7136031 1.401339 0.58741965 1.702360 0.93246077
#> 1009 814.522923 0.03503873 0.7136083 1.401329 0.58742642 1.702341 0.93249548
#> 1010 815.374675 0.03502042 0.7136135 1.401319 0.58743318 1.702321 0.93253013
#> 1011 816.226426 0.03500215 0.7136187 1.401308 0.58743993 1.702302 0.93256473
#> 1012 817.078178 0.03498390 0.7136239 1.401298 0.58744666 1.702282 0.93259927
#> 1013 817.929930 0.03496568 0.7136291 1.401288 0.58745338 1.702263 0.93263377
#> 1014 818.781682 0.03494749 0.7136343 1.401278 0.58746009 1.702243 0.93266821
#> 1015 819.633433 0.03492932 0.7136394 1.401268 0.58746678 1.702224 0.93270259
#> 1016 820.485185 0.03491119 0.7136446 1.401258 0.58747346 1.702205 0.93273692
#> 1017 821.336937 0.03489308 0.7136497 1.401248 0.58748013 1.702185 0.93277120
#> 1018 822.188689 0.03487500 0.7136548 1.401238 0.58748678 1.702166 0.93280543
#> 1019 823.040440 0.03485695 0.7136600 1.401228 0.58749342 1.702147 0.93283961
#> 1020 823.892192 0.03483893 0.7136651 1.401218 0.58750004 1.702128 0.93287373
#> 1021 824.743944 0.03482094 0.7136701 1.401208 0.58750665 1.702108 0.93290780
#> 1022 825.595696 0.03480297 0.7136752 1.401198 0.58751325 1.702089 0.93294182
#> 1023 826.447447 0.03478503 0.7136803 1.401188 0.58751983 1.702070 0.93297578
#> 1024 827.299199 0.03476712 0.7136854 1.401178 0.58752641 1.702051 0.93300970
#> 1025 828.150951 0.03474923 0.7136904 1.401168 0.58753296 1.702032 0.93304356
#> 1026 829.002703 0.03473138 0.7136955 1.401158 0.58753951 1.702013 0.93307737
#> 1027 829.854454 0.03471355 0.7137005 1.401148 0.58754604 1.701994 0.93311113
#> 1028 830.706206 0.03469575 0.7137055 1.401138 0.58755256 1.701975 0.93314484
#> 1029 831.557958 0.03467798 0.7137105 1.401128 0.58755906 1.701957 0.93317850
#> 1030 832.409710 0.03466023 0.7137155 1.401118 0.58756555 1.701938 0.93321210
#> 1031 833.261461 0.03464251 0.7137205 1.401109 0.58757203 1.701919 0.93324566
#> 1032 834.113213 0.03462482 0.7137255 1.401099 0.58757850 1.701900 0.93327916
#> 1033 834.964965 0.03460715 0.7137305 1.401089 0.58758495 1.701882 0.93331262
#> 1034 835.816717 0.03458952 0.7137354 1.401079 0.58759139 1.701863 0.93334602
#> 1035 836.668468 0.03457190 0.7137404 1.401070 0.58759782 1.701844 0.93337937
#> 1036 837.520220 0.03455432 0.7137453 1.401060 0.58760423 1.701826 0.93341268
#> 1037 838.371972 0.03453676 0.7137503 1.401050 0.58761063 1.701807 0.93344593
#> 1038 839.223724 0.03451923 0.7137552 1.401041 0.58761702 1.701789 0.93347913
#> 1039 840.075475 0.03450173 0.7137601 1.401031 0.58762340 1.701770 0.93351228
#> 1040 840.927227 0.03448425 0.7137650 1.401021 0.58762976 1.701752 0.93354538
#> 1041 841.778979 0.03446680 0.7137699 1.401012 0.58763611 1.701733 0.93357844
#> 1042 842.630731 0.03444938 0.7137748 1.401002 0.58764245 1.701715 0.93361144
#> 1043 843.482482 0.03443198 0.7137796 1.400993 0.58764877 1.701697 0.93364439
#> 1044 844.334234 0.03441461 0.7137845 1.400983 0.58765508 1.701678 0.93367730
#> 1045 845.185986 0.03439726 0.7137894 1.400974 0.58766138 1.701660 0.93371015
#> 1046 846.037738 0.03437994 0.7137942 1.400964 0.58766767 1.701642 0.93374296
#> 1047 846.889489 0.03436265 0.7137990 1.400955 0.58767395 1.701624 0.93377572
#> 1048 847.741241 0.03434538 0.7138039 1.400945 0.58768021 1.701606 0.93380843
#> 1049 848.592993 0.03432814 0.7138087 1.400936 0.58768646 1.701588 0.93384109
#> 1050 849.444745 0.03431093 0.7138135 1.400926 0.58769270 1.701570 0.93387370
#> 1051 850.296496 0.03429374 0.7138183 1.400917 0.58769892 1.701552 0.93390626
#> 1052 851.148248 0.03427657 0.7138231 1.400907 0.58770514 1.701534 0.93393877
#> 1053 851.720000 0.03426507 0.7138263 1.400901 0.58770930 1.701521 0.93396057
#> 1054 852.000000 0.03425944 0.7138278 1.400898 0.58771134 1.701516 0.93397124
#> ul95 ll998 ul998
#> 1 5.221912 0.001776962 8.584873
#> 2 3.662330 0.021035676 5.706165
#> 3 3.021377 0.054943422 4.534074
#> 4 2.664519 0.092282260 3.886543
#> 5 2.433992 0.128280000 3.470972
#> 6 2.271243 0.161498083 3.179229
#> 7 2.149350 0.191712021 2.961786
#> 8 2.054123 0.219103858 2.792643
#> 9 2.007393 0.233921516 2.709899
#> 10 1.977342 0.243969784 2.656786
#> 11 1.913897 0.266615301 2.544911
#> 12 1.860433 0.287319876 2.450931
#> 13 1.857410 0.288537829 2.445625
#> 14 1.814655 0.306327759 2.370690
#> 15 1.774933 0.323848461 2.301243
#> 16 1.740075 0.340060481 2.240449
#> 17 1.709190 0.355115736 2.186704
#> 18 1.681597 0.369143778 2.138787
#> 19 1.656766 0.382255470 2.095749
#> 20 1.634276 0.394546092 2.056839
#> 21 1.613791 0.406097904 2.021459
#> 22 1.595037 0.416982267 1.989120
#> 23 1.577789 0.427261369 1.959423
#> 24 1.561861 0.436989658 1.932039
#> 25 1.558062 0.439344427 1.925512
#> 26 1.547098 0.446215011 1.906690
#> 27 1.545079 0.447492114 1.903227
#> 28 1.533366 0.454979702 1.883143
#> 29 1.520554 0.463321211 1.861202
#> 30 1.508567 0.471272889 1.840695
#> 31 1.497321 0.478864524 1.821479
#> 32 1.486744 0.486122811 1.803427
#> 33 1.478364 0.491957528 1.789136
#> 34 1.476776 0.493071750 1.786429
#> 35 1.467359 0.499732987 1.770389
#> 36 1.458448 0.506126098 1.755222
#> 37 1.449998 0.512268838 1.740856
#> 38 1.441973 0.518177354 1.727222
#> 39 1.437947 0.521169050 1.720387
#> 40 1.434339 0.523866366 1.714264
#> 41 1.427065 0.529349324 1.701927
#> 42 1.420125 0.534638548 1.690166
#> 43 1.413670 0.539609377 1.679236
#> 44 1.413494 0.539745344 1.678938
#> 45 1.407151 0.544680112 1.668205
#> 46 1.401076 0.549452435 1.657933
#> 47 1.397536 0.552254441 1.651950
#> 48 1.395251 0.554071163 1.648089
#> 49 1.389659 0.558544479 1.638647
#> 50 1.384286 0.562879965 1.629580
#> 51 1.380998 0.565551484 1.624034
#> 52 1.379119 0.567084660 1.620864
#> 53 1.374143 0.571165104 1.612479
#> 54 1.369349 0.575127387 1.604403
#> 55 1.367468 0.576690571 1.601235
#> 56 1.367413 0.576735885 1.601144
#> 57 1.364726 0.578977185 1.596619
#> 58 1.360263 0.582719798 1.589111
#> 59 1.355953 0.586360182 1.581862
#> 60 1.351786 0.589902973 1.574859
#> 61 1.347755 0.593352518 1.568087
#> 62 1.343853 0.596712895 1.561536
#> 63 1.340074 0.599987936 1.555193
#> 64 1.336411 0.603181243 1.549048
#> 65 1.334400 0.604942106 1.545676
#> 66 1.332858 0.606296208 1.543091
#> 67 1.329410 0.609336030 1.537313
#> 68 1.326063 0.612303723 1.531706
#> 69 1.322810 0.615202136 1.526260
#> 70 1.319649 0.618033961 1.520970
#> 71 1.316575 0.620801744 1.515827
#> 72 1.313584 0.623507898 1.510825
#> 73 1.310673 0.626154707 1.505958
#> 74 1.307838 0.628744340 1.501220
#> 75 1.305456 0.630929146 1.497241
#> 76 1.305075 0.631278854 1.496606
#> 77 1.302383 0.633760204 1.492110
#> 78 1.299757 0.636190247 1.487728
#> 79 1.297196 0.638570754 1.483455
#> 80 1.294697 0.640903405 1.479286
#> 81 1.292257 0.643189806 1.475218
#> 82 1.289874 0.645431486 1.471246
#> 83 1.287546 0.647629903 1.467367
#> 84 1.285272 0.649786449 1.463578
#> 85 1.283048 0.651902455 1.459875
#> 86 1.280873 0.653979193 1.456255
#> 87 1.278745 0.656017877 1.452714
#> 88 1.276664 0.658019671 1.449251
#> 89 1.274626 0.659985689 1.445862
#> 90 1.272631 0.661916998 1.442545
#> 91 1.270677 0.663814621 1.439298
#> 92 1.268763 0.665679538 1.436117
#> 93 1.266888 0.667512691 1.433001
#> 94 1.265049 0.669314982 1.429948
#> 95 1.263247 0.671087278 1.426956
#> 96 1.261480 0.672830415 1.424022
#> 97 1.259746 0.674545191 1.421145
#> 98 1.258045 0.676232379 1.418323
#> 99 1.256939 0.677332525 1.416488
#> 100 1.256376 0.677892718 1.415555
#> 101 1.254738 0.679526923 1.412838
#> 102 1.253129 0.681135681 1.410171
#> 103 1.251550 0.682719654 1.407553
#> 104 1.249998 0.684279479 1.404982
#> 105 1.248474 0.685815771 1.402457
#> 106 1.246976 0.687329124 1.399977
#> 107 1.245505 0.688820110 1.397540
#> 108 1.244058 0.690289280 1.395145
#> 109 1.242636 0.691737169 1.392791
#> 110 1.241237 0.693164291 1.390476
#> 111 1.239861 0.694571145 1.388200
#> 112 1.238508 0.695958211 1.385962
#> 113 1.237177 0.697325954 1.383761
#> 114 1.235867 0.698674824 1.381595
#> 115 1.234578 0.700005257 1.379463
#> 116 1.233308 0.701317674 1.377366
#> 117 1.232059 0.702612481 1.375301
#> 118 1.230829 0.703890076 1.373269
#> 119 1.229617 0.705150839 1.371267
#> 120 1.228424 0.706395141 1.369297
#> 121 1.227248 0.707623343 1.367356
#> 122 1.226090 0.708835791 1.365444
#> 123 1.224949 0.710032825 1.363560
#> 124 1.223824 0.711214771 1.361704
#> 125 1.222716 0.712381947 1.359875
#> 126 1.221623 0.713534663 1.358072
#> 127 1.220545 0.714673217 1.356295
#> 128 1.219483 0.715797901 1.354543
#> 129 1.218435 0.716908997 1.352816
#> 130 1.217402 0.718006779 1.351113
#> 131 1.216383 0.719091515 1.349433
#> 132 1.215377 0.720163463 1.347776
#> 133 1.214385 0.721222876 1.346141
#> 134 1.213406 0.722269999 1.344528
#> 135 1.212440 0.723305071 1.342937
#> 136 1.211487 0.724328322 1.341367
#> 137 1.210546 0.725339980 1.339817
#> 138 1.209617 0.726340263 1.338288
#> 139 1.208700 0.727329386 1.336778
#> 140 1.207794 0.728307557 1.335287
#> 141 1.206900 0.729274979 1.333815
#> 142 1.206016 0.730231849 1.332362
#> 143 1.205144 0.731178360 1.330926
#> 144 1.204282 0.732114699 1.329509
#> 145 1.203997 0.732424700 1.329040
#> 146 1.203431 0.733041049 1.328109
#> 147 1.202590 0.733957589 1.326726
#> 148 1.201759 0.734864492 1.325359
#> 149 1.200937 0.735761928 1.324009
#> 150 1.200126 0.736650063 1.322675
#> 151 1.199324 0.737529056 1.321356
#> 152 1.198531 0.738399066 1.320054
#> 153 1.197747 0.739260247 1.318766
#> 154 1.197455 0.739581549 1.318286
#> 155 1.196972 0.740112748 1.317493
#> 156 1.196206 0.740956716 1.316234
#> 157 1.195449 0.741792293 1.314990
#> 158 1.194925 0.742370853 1.314130
#> 159 1.194700 0.742619619 1.313760
#> 160 1.193959 0.743438831 1.312544
#> 161 1.193227 0.744250061 1.311341
#> 162 1.192502 0.745053440 1.310152
#> 163 1.191785 0.745849095 1.308975
#> 164 1.191076 0.746637150 1.307812
#> 165 1.190375 0.747417726 1.306661
#> 166 1.189681 0.748190943 1.305522
#> 167 1.188994 0.748956916 1.304395
#> 168 1.188315 0.749715759 1.303281
#> 169 1.187643 0.750467583 1.302178
#> 170 1.186977 0.751212496 1.301086
#> 171 1.186319 0.751950606 1.300006
#> 172 1.185667 0.752682015 1.298937
#> 173 1.185021 0.753406826 1.297879
#> 174 1.184383 0.754125139 1.296832
#> 175 1.183750 0.754837050 1.295795
#> 176 1.183124 0.755542655 1.294769
#> 177 1.182504 0.756242048 1.293753
#> 178 1.181890 0.756935320 1.292747
#> 179 1.181282 0.757622561 1.291751
#> 180 1.180680 0.758303859 1.290765
#> 181 1.180084 0.758979299 1.289788
#> 182 1.179494 0.759648966 1.288821
#> 183 1.178909 0.760312943 1.287863
#> 184 1.178329 0.760971310 1.286914
#> 185 1.177755 0.761624147 1.285974
#> 186 1.177187 0.762271532 1.285043
#> 187 1.176624 0.762913540 1.284121
#> 188 1.176214 0.763380477 1.283451
#> 189 1.176065 0.763550246 1.283207
#> 190 1.175512 0.764181724 1.282302
#> 191 1.174964 0.764808046 1.281405
#> 192 1.174421 0.765429282 1.280517
#> 193 1.173883 0.766045501 1.279636
#> 194 1.173350 0.766656770 1.278764
#> 195 1.172822 0.767263158 1.277899
#> 196 1.172298 0.767864727 1.277042
#> 197 1.171778 0.768461544 1.276193
#> 198 1.171264 0.769053670 1.275351
#> 199 1.170754 0.769641168 1.274516
#> 200 1.170608 0.769809092 1.274278
#> 201 1.170248 0.770224097 1.273689
#> 202 1.170116 0.770375923 1.273474
#> 203 1.169746 0.770802518 1.272869
#> 204 1.169249 0.771376488 1.272056
#> 205 1.168756 0.771946066 1.271250
#> 206 1.168267 0.772511306 1.270451
#> 207 1.167783 0.773072266 1.269659
#> 208 1.167302 0.773628997 1.268874
#> 209 1.166826 0.774181555 1.268095
#> 210 1.166353 0.774729992 1.267322
#> 211 1.165884 0.775274358 1.266556
#> 212 1.165419 0.775814705 1.265797
#> 213 1.164958 0.776351082 1.265043
#> 214 1.164501 0.776883539 1.264296
#> 215 1.164047 0.777412122 1.263555
#> 216 1.163597 0.777936879 1.262820
#> 217 1.163150 0.778457856 1.262091
#> 218 1.162707 0.778975100 1.261367
#> 219 1.162268 0.779488654 1.260650
#> 220 1.161832 0.779998563 1.259938
#> 221 1.161399 0.780504871 1.259231
#> 222 1.160970 0.781007619 1.258531
#> 223 1.160931 0.781053422 1.258467
#> 224 1.160544 0.781506850 1.257835
#> 225 1.160122 0.782002604 1.257146
#> 226 1.159702 0.782494923 1.256461
#> 227 1.159286 0.782983846 1.255782
#> 228 1.158873 0.783469413 1.255108
#> 229 1.158463 0.783951661 1.254439
#> 230 1.158056 0.784430629 1.253775
#> 231 1.157653 0.784906355 1.253116
#> 232 1.157252 0.785378874 1.252462
#> 233 1.156854 0.785848224 1.251813
#> 234 1.156719 0.786007517 1.251593
#> 235 1.156459 0.786314439 1.251169
#> 236 1.156067 0.786777555 1.250530
#> 237 1.155678 0.787237607 1.249895
#> 238 1.155292 0.787694627 1.249265
#> 239 1.154908 0.788148651 1.248640
#> 240 1.154528 0.788599709 1.248019
#> 241 1.154203 0.788983890 1.247490
#> 242 1.154149 0.789047836 1.247403
#> 243 1.153774 0.789493063 1.246791
#> 244 1.153402 0.789935420 1.246183
#> 245 1.153208 0.790165202 1.245868
#> 246 1.153031 0.790374940 1.245580
#> 247 1.152664 0.790811653 1.244981
#> 248 1.152299 0.791245588 1.244386
#> 249 1.151937 0.791676776 1.243796
#> 250 1.151577 0.792105245 1.243209
#> 251 1.151220 0.792531024 1.242627
#> 252 1.150865 0.792954141 1.242049
#> 253 1.150512 0.793374624 1.241474
#> 254 1.150162 0.793792502 1.240904
#> 255 1.149815 0.794207799 1.240338
#> 256 1.149469 0.794620544 1.239775
#> 257 1.149126 0.795030763 1.239216
#> 258 1.149033 0.795142828 1.239064
#> 259 1.148786 0.795438481 1.238661
#> 260 1.148447 0.795843724 1.238110
#> 261 1.148111 0.796246517 1.237562
#> 262 1.147777 0.796646885 1.237019
#> 263 1.147445 0.797044852 1.236478
#> 264 1.147116 0.797440443 1.235942
#> 265 1.146788 0.797833681 1.235408
#> 266 1.146463 0.798224590 1.234879
#> 267 1.146140 0.798613192 1.234353
#> 268 1.145819 0.798999511 1.233830
#> 269 1.145500 0.799383568 1.233310
#> 270 1.145183 0.799765387 1.232794
#> 271 1.144868 0.800144989 1.232281
#> 272 1.144555 0.800522395 1.231772
#> 273 1.144244 0.800897627 1.231266
#> 274 1.143935 0.801270706 1.230763
#> 275 1.143932 0.801273137 1.230759
#> 276 1.143627 0.801641652 1.230263
#> 277 1.143322 0.802010486 1.229766
#> 278 1.143019 0.802377228 1.229273
#> 279 1.142717 0.802741898 1.228782
#> 280 1.142418 0.803104515 1.228295
#> 281 1.142120 0.803465099 1.227810
#> 282 1.141824 0.803823668 1.227329
#> 283 1.141530 0.804180242 1.226850
#> 284 1.141237 0.804534840 1.226375
#> 285 1.140947 0.804887479 1.225902
#> 286 1.140658 0.805238178 1.225432
#> 287 1.140371 0.805586954 1.224965
#> 288 1.140085 0.805933825 1.224501
#> 289 1.139802 0.806278810 1.224040
#> 290 1.139520 0.806621923 1.223581
#> 291 1.139239 0.806963184 1.223125
#> 292 1.138961 0.807302608 1.222672
#> 293 1.138683 0.807640212 1.222221
#> 294 1.138408 0.807976013 1.221773
#> 295 1.138134 0.808310026 1.221328
#> 296 1.137862 0.808642268 1.220885
#> 297 1.137591 0.808972754 1.220445
#> 298 1.137322 0.809301499 1.220008
#> 299 1.137054 0.809628520 1.219573
#> 300 1.136788 0.809953830 1.219140
#> 301 1.136523 0.810277446 1.218710
#> 302 1.136260 0.810599382 1.218283
#> 303 1.135999 0.810919652 1.217858
#> 304 1.135739 0.811238272 1.217435
#> 305 1.135480 0.811555254 1.217014
#> 306 1.135223 0.811870614 1.216597
#> 307 1.134967 0.812184365 1.216181
#> 308 1.134712 0.812496521 1.215768
#> 309 1.134459 0.812807095 1.215357
#> 310 1.134242 0.813074202 1.215003
#> 311 1.134208 0.813116102 1.214948
#> 312 1.133957 0.813423553 1.214541
#> 313 1.133709 0.813729463 1.214137
#> 314 1.133461 0.814033844 1.213735
#> 315 1.133215 0.814336709 1.213335
#> 316 1.133198 0.814357011 1.213308
#> 317 1.132970 0.814638070 1.212938
#> 318 1.132727 0.814937941 1.212542
#> 319 1.132484 0.815236333 1.212149
#> 320 1.132243 0.815533259 1.211757
#> 321 1.132004 0.815828730 1.211368
#> 322 1.131898 0.815959564 1.211196
#> 323 1.131765 0.816122760 1.210981
#> 324 1.131528 0.816415358 1.210596
#> 325 1.131292 0.816706538 1.210213
#> 326 1.131058 0.816996310 1.209832
#> 327 1.130824 0.817284686 1.209453
#> 328 1.130592 0.817571678 1.209076
#> 329 1.130395 0.817815875 1.208756
#> 330 1.130361 0.817857296 1.208702
#> 331 1.130131 0.818141551 1.208329
#> 332 1.129903 0.818424454 1.207958
#> 333 1.129675 0.818706017 1.207588
#> 334 1.129449 0.818986249 1.207221
#> 335 1.129224 0.819265161 1.206856
#> 336 1.129000 0.819542764 1.206492
#> 337 1.128777 0.819819068 1.206131
#> 338 1.128555 0.820094082 1.205771
#> 339 1.128335 0.820367818 1.205413
#> 340 1.128304 0.820406429 1.205363
#> 341 1.128115 0.820640285 1.205057
#> 342 1.127897 0.820911493 1.204703
#> 343 1.127680 0.821181452 1.204350
#> 344 1.127464 0.821450170 1.204000
#> 345 1.127248 0.821717659 1.203651
#> 346 1.127034 0.821983927 1.203303
#> 347 1.126821 0.822248983 1.202958
#> 348 1.126609 0.822512837 1.202614
#> 349 1.126398 0.822775499 1.202272
#> 350 1.126189 0.823036976 1.201931
#> 351 1.125980 0.823297277 1.201593
#> 352 1.125850 0.823459023 1.201382
#> 353 1.125772 0.823556413 1.201256
#> 354 1.125565 0.823814391 1.200920
#> 355 1.125359 0.824071220 1.200586
#> 356 1.125154 0.824326909 1.200254
#> 357 1.124950 0.824581466 1.199923
#> 358 1.124747 0.824834900 1.199594
#> 359 1.124546 0.825087218 1.199267
#> 360 1.124378 0.825296383 1.198996
#> 361 1.124345 0.825338429 1.198941
#> 362 1.124145 0.825588542 1.198617
#> 363 1.123945 0.825837564 1.198294
#> 364 1.123747 0.826085503 1.197973
#> 365 1.123550 0.826332367 1.197653
#> 366 1.123354 0.826578164 1.197335
#> 367 1.123158 0.826822901 1.197018
#> 368 1.122964 0.827066587 1.196703
#> 369 1.122951 0.827082262 1.196683
#> 370 1.122770 0.827309229 1.196389
#> 371 1.122578 0.827550834 1.196077
#> 372 1.122386 0.827791409 1.195766
#> 373 1.122195 0.828030963 1.195457
#> 374 1.122005 0.828269501 1.195149
#> 375 1.121816 0.828507033 1.194842
#> 376 1.121627 0.828743564 1.194537
#> 377 1.121440 0.828979101 1.194233
#> 378 1.121253 0.829213653 1.193931
#> 379 1.121067 0.829447224 1.193630
#> 380 1.120883 0.829679824 1.193330
#> 381 1.120698 0.829911457 1.193032
#> 382 1.120515 0.830142131 1.192735
#> 383 1.120333 0.830371853 1.192439
#> 384 1.120151 0.830600629 1.192145
#> 385 1.119970 0.830828466 1.191852
#> 386 1.119790 0.831055370 1.191560
#> 387 1.119611 0.831281347 1.191270
#> 388 1.119432 0.831506404 1.190981
#> 389 1.119303 0.831670079 1.190770
#> 390 1.119255 0.831730547 1.190693
#> 391 1.119078 0.831953783 1.190406
#> 392 1.118902 0.832176116 1.190121
#> 393 1.118726 0.832397555 1.189837
#> 394 1.118552 0.832618104 1.189554
#> 395 1.118378 0.832837770 1.189273
#> 396 1.118205 0.833056558 1.188992
#> 397 1.118032 0.833274474 1.188713
#> 398 1.117860 0.833491525 1.188435
#> 399 1.117690 0.833707715 1.188158
#> 400 1.117519 0.833923052 1.187883
#> 401 1.117350 0.834137539 1.187608
#> 402 1.117181 0.834351183 1.187335
#> 403 1.117013 0.834563990 1.187063
#> 404 1.116846 0.834775965 1.186792
#> 405 1.116679 0.834987113 1.186523
#> 406 1.116513 0.835197440 1.186254
#> 407 1.116348 0.835406951 1.185986
#> 408 1.116184 0.835615651 1.185720
#> 409 1.116020 0.835823546 1.185455
#> 410 1.115856 0.836030641 1.185191
#> 411 1.115694 0.836236941 1.184928
#> 412 1.115532 0.836442450 1.184666
#> 413 1.115437 0.836563046 1.184512
#> 414 1.115371 0.836647176 1.184405
#> 415 1.115210 0.836851121 1.184145
#> 416 1.115051 0.837054291 1.183886
#> 417 1.114891 0.837256692 1.183629
#> 418 1.114733 0.837458327 1.183372
#> 419 1.114575 0.837659203 1.183117
#> 420 1.114418 0.837859323 1.182862
#> 421 1.114261 0.838058692 1.182609
#> 422 1.114105 0.838257315 1.182356
#> 423 1.113950 0.838455198 1.182105
#> 424 1.113795 0.838652343 1.181854
#> 425 1.113641 0.838848757 1.181605
#> 426 1.113487 0.839044443 1.181357
#> 427 1.113334 0.839239406 1.181109
#> 428 1.113182 0.839433650 1.180863
#> 429 1.113030 0.839627180 1.180617
#> 430 1.112879 0.839820001 1.180373
#> 431 1.112729 0.840012117 1.180129
#> 432 1.112579 0.840203531 1.179887
#> 433 1.112429 0.840394249 1.179645
#> 434 1.112280 0.840584274 1.179405
#> 435 1.112132 0.840773611 1.179165
#> 436 1.111985 0.840962263 1.178926
#> 437 1.111838 0.841150236 1.178688
#> 438 1.111691 0.841337533 1.178451
#> 439 1.111545 0.841524158 1.178215
#> 440 1.111400 0.841710116 1.177980
#> 441 1.111255 0.841895409 1.177746
#> 442 1.111111 0.842080043 1.177513
#> 443 1.110967 0.842264021 1.177281
#> 444 1.110861 0.842399421 1.177110
#> 445 1.110824 0.842447347 1.177049
#> 446 1.110681 0.842630025 1.176819
#> 447 1.110539 0.842812058 1.176589
#> 448 1.110398 0.842993452 1.176360
#> 449 1.110257 0.843174208 1.176132
#> 450 1.110116 0.843354331 1.175905
#> 451 1.109976 0.843533826 1.175679
#> 452 1.109837 0.843712694 1.175453
#> 453 1.109698 0.843890941 1.175229
#> 454 1.109560 0.844068569 1.175005
#> 455 1.109422 0.844245583 1.174782
#> 456 1.109284 0.844421985 1.174560
#> 457 1.109148 0.844597780 1.174339
#> 458 1.109011 0.844772971 1.174119
#> 459 1.108875 0.844947561 1.173899
#> 460 1.108802 0.845042116 1.173780
#> 461 1.108740 0.845121554 1.173680
#> 462 1.108605 0.845294953 1.173462
#> 463 1.108474 0.845463155 1.173251
#> 464 1.108471 0.845467762 1.173245
#> 465 1.108337 0.845639984 1.173029
#> 466 1.108204 0.845811622 1.172813
#> 467 1.108071 0.845982679 1.172598
#> 468 1.107938 0.846153160 1.172384
#> 469 1.107806 0.846323067 1.172171
#> 470 1.107675 0.846492403 1.171959
#> 471 1.107544 0.846661171 1.171747
#> 472 1.107413 0.846829376 1.171536
#> 473 1.107283 0.846997019 1.171326
#> 474 1.107154 0.847164105 1.171116
#> 475 1.107024 0.847330635 1.170908
#> 476 1.106896 0.847496614 1.170700
#> 477 1.106768 0.847662045 1.170493
#> 478 1.106640 0.847826929 1.170286
#> 479 1.106512 0.847991271 1.170081
#> 480 1.106386 0.848155073 1.169876
#> 481 1.106259 0.848318339 1.169671
#> 482 1.106133 0.848481071 1.169468
#> 483 1.106008 0.848643272 1.169265
#> 484 1.105882 0.848804945 1.169063
#> 485 1.105758 0.848966093 1.168861
#> 486 1.105633 0.849126719 1.168661
#> 487 1.105510 0.849286826 1.168461
#> 488 1.105386 0.849446416 1.168261
#> 489 1.105263 0.849605492 1.168063
#> 490 1.105141 0.849764057 1.167865
#> 491 1.105019 0.849922114 1.167668
#> 492 1.104897 0.850079666 1.167471
#> 493 1.104776 0.850236714 1.167275
#> 494 1.104655 0.850393263 1.167080
#> 495 1.104534 0.850549314 1.166885
#> 496 1.104414 0.850704870 1.166691
#> 497 1.104295 0.850859934 1.166498
#> 498 1.104175 0.851014509 1.166306
#> 499 1.104056 0.851168596 1.166114
#> 500 1.103938 0.851322199 1.165922
#> 501 1.103820 0.851475320 1.165732
#> 502 1.103702 0.851627962 1.165542
#> 503 1.103585 0.851780127 1.165353
#> 504 1.103468 0.851931817 1.165164
#> 505 1.103352 0.852083036 1.164976
#> 506 1.103236 0.852233785 1.164788
#> 507 1.103120 0.852384068 1.164601
#> 508 1.103004 0.852533885 1.164415
#> 509 1.102890 0.852683241 1.164230
#> 510 1.102775 0.852832137 1.164045
#> 511 1.102661 0.852980575 1.163860
#> 512 1.102547 0.853128558 1.163677
#> 513 1.102433 0.853276089 1.163493
#> 514 1.102320 0.853423169 1.163311
#> 515 1.102208 0.853569801 1.163129
#> 516 1.102095 0.853715988 1.162948
#> 517 1.101983 0.853861730 1.162767
#> 518 1.101872 0.854007032 1.162587
#> 519 1.101760 0.854151894 1.162407
#> 520 1.101649 0.854296320 1.162228
#> 521 1.101621 0.854333411 1.162182
#> 522 1.101539 0.854440311 1.162050
#> 523 1.101429 0.854583869 1.161872
#> 524 1.101319 0.854726997 1.161694
#> 525 1.101209 0.854869697 1.161518
#> 526 1.101144 0.854955296 1.161412
#> 527 1.101100 0.855011971 1.161342
#> 528 1.100991 0.855153821 1.161166
#> 529 1.100883 0.855295250 1.160991
#> 530 1.100775 0.855436259 1.160816
#> 531 1.100667 0.855576850 1.160643
#> 532 1.100560 0.855717026 1.160469
#> 533 1.100452 0.855856788 1.160296
#> 534 1.100346 0.855996139 1.160124
#> 535 1.100239 0.856135081 1.159952
#> 536 1.100133 0.856273615 1.159781
#> 537 1.100027 0.856411744 1.159611
#> 538 1.099922 0.856549469 1.159440
#> 539 1.099817 0.856686793 1.159271
#> 540 1.099712 0.856823718 1.159102
#> 541 1.099608 0.856960245 1.158933
#> 542 1.099503 0.857096377 1.158765
#> 543 1.099400 0.857232115 1.158598
#> 544 1.099296 0.857367461 1.158431
#> 545 1.099193 0.857502417 1.158264
#> 546 1.099090 0.857636986 1.158098
#> 547 1.098988 0.857771168 1.157933
#> 548 1.098885 0.857904966 1.157768
#> 549 1.098783 0.858038382 1.157604
#> 550 1.098682 0.858171417 1.157440
#> 551 1.098580 0.858304073 1.157276
#> 552 1.098479 0.858436352 1.157113
#> 553 1.098379 0.858568257 1.156951
#> 554 1.098278 0.858699787 1.156789
#> 555 1.098178 0.858830946 1.156628
#> 556 1.098079 0.858961736 1.156467
#> 557 1.097979 0.859092157 1.156306
#> 558 1.097880 0.859222212 1.156146
#> 559 1.097781 0.859351902 1.155987
#> 560 1.097682 0.859481229 1.155828
#> 561 1.097584 0.859610195 1.155669
#> 562 1.097486 0.859738801 1.155511
#> 563 1.097388 0.859867049 1.155354
#> 564 1.097361 0.859902722 1.155310
#> 565 1.097291 0.859994942 1.155196
#> 566 1.097194 0.860122479 1.155040
#> 567 1.097097 0.860249664 1.154884
#> 568 1.097000 0.860376497 1.154728
#> 569 1.096904 0.860502981 1.154573
#> 570 1.096829 0.860602020 1.154451
#> 571 1.096808 0.860629117 1.154418
#> 572 1.096712 0.860754906 1.154263
#> 573 1.096617 0.860880350 1.154110
#> 574 1.096522 0.861005452 1.153956
#> 575 1.096427 0.861130211 1.153803
#> 576 1.096332 0.861254630 1.153650
#> 577 1.096238 0.861378711 1.153498
#> 578 1.096144 0.861502455 1.153347
#> 579 1.096050 0.861625863 1.153195
#> 580 1.095956 0.861748937 1.153045
#> 581 1.095863 0.861871679 1.152894
#> 582 1.095770 0.861994089 1.152744
#> 583 1.095677 0.862116170 1.152595
#> 584 1.095585 0.862237923 1.152446
#> 585 1.095492 0.862359350 1.152297
#> 586 1.095401 0.862480452 1.152149
#> 587 1.095309 0.862601230 1.152001
#> 588 1.095217 0.862721685 1.151854
#> 589 1.095126 0.862841821 1.151707
#> 590 1.095035 0.862961636 1.151560
#> 591 1.094945 0.863081134 1.151414
#> 592 1.094854 0.863200316 1.151268
#> 593 1.094764 0.863319182 1.151123
#> 594 1.094674 0.863437735 1.150978
#> 595 1.094585 0.863555975 1.150834
#> 596 1.094495 0.863673905 1.150690
#> 597 1.094406 0.863791525 1.150546
#> 598 1.094317 0.863908837 1.150403
#> 599 1.094228 0.864025842 1.150260
#> 600 1.094140 0.864142541 1.150118
#> 601 1.094104 0.864189863 1.150060
#> 602 1.094052 0.864258936 1.149975
#> 603 1.093964 0.864375029 1.149834
#> 604 1.093876 0.864490820 1.149692
#> 605 1.093789 0.864606311 1.149552
#> 606 1.093702 0.864721503 1.149411
#> 607 1.093615 0.864836397 1.149271
#> 608 1.093528 0.864950995 1.149131
#> 609 1.093442 0.865065298 1.148992
#> 610 1.093355 0.865179307 1.148853
#> 611 1.093269 0.865293024 1.148714
#> 612 1.093184 0.865406449 1.148576
#> 613 1.093117 0.865495037 1.148468
#> 614 1.093098 0.865519585 1.148438
#> 615 1.093013 0.865632431 1.148301
#> 616 1.092928 0.865744990 1.148164
#> 617 1.092843 0.865857263 1.148027
#> 618 1.092758 0.865969251 1.147891
#> 619 1.092674 0.866080955 1.147755
#> 620 1.092590 0.866192376 1.147619
#> 621 1.092506 0.866303516 1.147484
#> 622 1.092422 0.866414375 1.147349
#> 623 1.092338 0.866524956 1.147215
#> 624 1.092255 0.866635258 1.147081
#> 625 1.092172 0.866745284 1.146947
#> 626 1.092089 0.866855034 1.146813
#> 627 1.092007 0.866964510 1.146680
#> 628 1.091924 0.867073712 1.146548
#> 629 1.091842 0.867182642 1.146415
#> 630 1.091760 0.867291302 1.146283
#> 631 1.091678 0.867399691 1.146152
#> 632 1.091597 0.867507812 1.146020
#> 633 1.091516 0.867615664 1.145889
#> 634 1.091434 0.867723251 1.145759
#> 635 1.091354 0.867830572 1.145628
#> 636 1.091273 0.867937628 1.145499
#> 637 1.091192 0.868044422 1.145369
#> 638 1.091112 0.868150953 1.145240
#> 639 1.091032 0.868257223 1.145111
#> 640 1.090952 0.868363233 1.144982
#> 641 1.090873 0.868468984 1.144854
#> 642 1.090793 0.868574477 1.144726
#> 643 1.090714 0.868679714 1.144599
#> 644 1.090635 0.868784694 1.144471
#> 645 1.090556 0.868889420 1.144344
#> 646 1.090478 0.868993892 1.144218
#> 647 1.090399 0.869098111 1.144091
#> 648 1.090321 0.869202079 1.143966
#> 649 1.090243 0.869305796 1.143840
#> 650 1.090165 0.869409263 1.143715
#> 651 1.090087 0.869512482 1.143590
#> 652 1.090010 0.869615453 1.143465
#> 653 1.089933 0.869718178 1.143341
#> 654 1.089856 0.869820656 1.143217
#> 655 1.089779 0.869922890 1.143093
#> 656 1.089702 0.870024881 1.142970
#> 657 1.089626 0.870126628 1.142847
#> 658 1.089550 0.870228134 1.142724
#> 659 1.089474 0.870329399 1.142601
#> 660 1.089431 0.870385907 1.142533
#> 661 1.089398 0.870430425 1.142479
#> 662 1.089322 0.870531211 1.142357
#> 663 1.089247 0.870631759 1.142236
#> 664 1.089171 0.870732071 1.142115
#> 665 1.089096 0.870832146 1.141994
#> 666 1.089021 0.870931986 1.141873
#> 667 1.088946 0.871031592 1.141753
#> 668 1.088872 0.871130965 1.141633
#> 669 1.088798 0.871230105 1.141513
#> 670 1.088723 0.871329013 1.141394
#> 671 1.088649 0.871427692 1.141274
#> 672 1.088576 0.871526140 1.141156
#> 673 1.088502 0.871624360 1.141037
#> 674 1.088428 0.871722352 1.140919
#> 675 1.088355 0.871820116 1.140801
#> 676 1.088282 0.871917655 1.140683
#> 677 1.088209 0.872014968 1.140566
#> 678 1.088136 0.872112057 1.140449
#> 679 1.088064 0.872208923 1.140332
#> 680 1.087991 0.872305566 1.140216
#> 681 1.087919 0.872401987 1.140099
#> 682 1.087847 0.872498187 1.139983
#> 683 1.087775 0.872594167 1.139868
#> 684 1.087704 0.872689928 1.139752
#> 685 1.087632 0.872785470 1.139637
#> 686 1.087561 0.872880795 1.139522
#> 687 1.087490 0.872975903 1.139408
#> 688 1.087419 0.873070795 1.139294
#> 689 1.087348 0.873165471 1.139180
#> 690 1.087277 0.873259934 1.139066
#> 691 1.087207 0.873354183 1.138953
#> 692 1.087136 0.873448219 1.138839
#> 693 1.087066 0.873542044 1.138726
#> 694 1.086996 0.873635657 1.138614
#> 695 1.086926 0.873729061 1.138501
#> 696 1.086857 0.873822254 1.138389
#> 697 1.086816 0.873876112 1.138325
#> 698 1.086787 0.873915239 1.138278
#> 699 1.086718 0.874008016 1.138166
#> 700 1.086649 0.874100586 1.138055
#> 701 1.086580 0.874192950 1.137944
#> 702 1.086511 0.874285107 1.137833
#> 703 1.086442 0.874377061 1.137722
#> 704 1.086374 0.874468809 1.137612
#> 705 1.086305 0.874560355 1.137502
#> 706 1.086237 0.874651698 1.137392
#> 707 1.086169 0.874742839 1.137283
#> 708 1.086101 0.874833780 1.137174
#> 709 1.086033 0.874924519 1.137065
#> 710 1.085966 0.875015060 1.136956
#> 711 1.085898 0.875105401 1.136848
#> 712 1.085831 0.875195544 1.136739
#> 713 1.085764 0.875285490 1.136632
#> 714 1.085697 0.875375239 1.136524
#> 715 1.085630 0.875464793 1.136416
#> 716 1.085564 0.875554151 1.136309
#> 717 1.085497 0.875643314 1.136202
#> 718 1.085431 0.875732284 1.136096
#> 719 1.085365 0.875821060 1.135989
#> 720 1.085299 0.875909644 1.135883
#> 721 1.085233 0.875998037 1.135777
#> 722 1.085167 0.876086238 1.135671
#> 723 1.085101 0.876174249 1.135566
#> 724 1.085036 0.876262070 1.135461
#> 725 1.084971 0.876349703 1.135356
#> 726 1.084906 0.876437147 1.135251
#> 727 1.084841 0.876524403 1.135146
#> 728 1.084776 0.876611473 1.135042
#> 729 1.084711 0.876698356 1.134938
#> 730 1.084646 0.876785054 1.134834
#> 731 1.084582 0.876871567 1.134731
#> 732 1.084518 0.876957895 1.134627
#> 733 1.084454 0.877044040 1.134524
#> 734 1.084390 0.877130002 1.134421
#> 735 1.084326 0.877215782 1.134319
#> 736 1.084262 0.877301380 1.134216
#> 737 1.084199 0.877386797 1.134114
#> 738 1.084135 0.877472033 1.134012
#> 739 1.084072 0.877557090 1.133910
#> 740 1.084009 0.877641968 1.133809
#> 741 1.083946 0.877726667 1.133708
#> 742 1.083883 0.877811188 1.133607
#> 743 1.083820 0.877895532 1.133506
#> 744 1.083758 0.877979700 1.133405
#> 745 1.083695 0.878063691 1.133305
#> 746 1.083633 0.878147507 1.133205
#> 747 1.083571 0.878231149 1.133105
#> 748 1.083509 0.878314616 1.133005
#> 749 1.083447 0.878397909 1.132906
#> 750 1.083385 0.878481030 1.132806
#> 751 1.083324 0.878563979 1.132707
#> 752 1.083262 0.878646755 1.132608
#> 753 1.083201 0.878729361 1.132510
#> 754 1.083140 0.878811796 1.132411
#> 755 1.083079 0.878894061 1.132313
#> 756 1.083018 0.878976156 1.132215
#> 757 1.082957 0.879058083 1.132118
#> 758 1.082896 0.879139842 1.132020
#> 759 1.082836 0.879221432 1.131923
#> 760 1.082775 0.879302856 1.131826
#> 761 1.082715 0.879384114 1.131729
#> 762 1.082655 0.879465205 1.131632
#> 763 1.082595 0.879546131 1.131535
#> 764 1.082535 0.879626892 1.131439
#> 765 1.082475 0.879707490 1.131343
#> 766 1.082416 0.879787923 1.131247
#> 767 1.082393 0.879818311 1.131211
#> 768 1.082356 0.879868193 1.131152
#> 769 1.082297 0.879948301 1.131056
#> 770 1.082237 0.880028247 1.130961
#> 771 1.082178 0.880108031 1.130866
#> 772 1.082132 0.880171166 1.130791
#> 773 1.082119 0.880187654 1.130771
#> 774 1.082060 0.880267117 1.130676
#> 775 1.082002 0.880346420 1.130582
#> 776 1.081958 0.880405901 1.130511
#> 777 1.081943 0.880425564 1.130488
#> 778 1.081885 0.880504549 1.130394
#> 779 1.081826 0.880583376 1.130300
#> 780 1.081768 0.880662045 1.130206
#> 781 1.081710 0.880740557 1.130113
#> 782 1.081652 0.880818912 1.130019
#> 783 1.081594 0.880897111 1.129926
#> 784 1.081536 0.880975155 1.129834
#> 785 1.081489 0.881038809 1.129758
#> 786 1.081478 0.881053043 1.129741
#> 787 1.081421 0.881130777 1.129648
#> 788 1.081364 0.881208357 1.129556
#> 789 1.081306 0.881285783 1.129464
#> 790 1.081249 0.881363056 1.129372
#> 791 1.081192 0.881440177 1.129281
#> 792 1.081135 0.881517146 1.129189
#> 793 1.081078 0.881593963 1.129098
#> 794 1.081022 0.881670629 1.129007
#> 795 1.080965 0.881747145 1.128916
#> 796 1.080909 0.881823510 1.128825
#> 797 1.080852 0.881899726 1.128734
#> 798 1.080796 0.881975793 1.128644
#> 799 1.080740 0.882051711 1.128554
#> 800 1.080684 0.882127482 1.128464
#> 801 1.080628 0.882203104 1.128374
#> 802 1.080572 0.882278580 1.128285
#> 803 1.080517 0.882353909 1.128195
#> 804 1.080461 0.882429092 1.128106
#> 805 1.080406 0.882504129 1.128017
#> 806 1.080350 0.882579021 1.127928
#> 807 1.080295 0.882653768 1.127839
#> 808 1.080240 0.882728370 1.127751
#> 809 1.080185 0.882802829 1.127662
#> 810 1.080130 0.882877145 1.127574
#> 811 1.080075 0.882951318 1.127486
#> 812 1.080021 0.883025348 1.127398
#> 813 1.079966 0.883099237 1.127311
#> 814 1.079912 0.883172983 1.127223
#> 815 1.079857 0.883246589 1.127136
#> 816 1.079803 0.883320054 1.127049
#> 817 1.079749 0.883393379 1.126962
#> 818 1.079695 0.883466565 1.126875
#> 819 1.079641 0.883539611 1.126789
#> 820 1.079587 0.883612518 1.126702
#> 821 1.079534 0.883685287 1.126616
#> 822 1.079480 0.883757918 1.126530
#> 823 1.079427 0.883830411 1.126444
#> 824 1.079373 0.883902767 1.126359
#> 825 1.079320 0.883974987 1.126273
#> 826 1.079267 0.884047070 1.126188
#> 827 1.079214 0.884119018 1.126102
#> 828 1.079161 0.884190830 1.126017
#> 829 1.079108 0.884262507 1.125933
#> 830 1.079056 0.884334050 1.125848
#> 831 1.079003 0.884405459 1.125763
#> 832 1.078950 0.884476734 1.125679
#> 833 1.078898 0.884547876 1.125595
#> 834 1.078846 0.884618885 1.125511
#> 835 1.078793 0.884689762 1.125427
#> 836 1.078741 0.884760506 1.125343
#> 837 1.078689 0.884831120 1.125260
#> 838 1.078638 0.884901601 1.125176
#> 839 1.078586 0.884971953 1.125093
#> 840 1.078534 0.885042173 1.125010
#> 841 1.078482 0.885112264 1.124927
#> 842 1.078431 0.885182225 1.124845
#> 843 1.078380 0.885252057 1.124762
#> 844 1.078328 0.885321761 1.124680
#> 845 1.078277 0.885391336 1.124598
#> 846 1.078226 0.885460783 1.124516
#> 847 1.078175 0.885530102 1.124434
#> 848 1.078124 0.885599294 1.124352
#> 849 1.078073 0.885668360 1.124270
#> 850 1.078023 0.885737299 1.124189
#> 851 1.077972 0.885806112 1.124108
#> 852 1.077921 0.885874799 1.124026
#> 853 1.077871 0.885943362 1.123946
#> 854 1.077821 0.886011799 1.123865
#> 855 1.077771 0.886080112 1.123784
#> 856 1.077739 0.886122824 1.123734
#> 857 1.077720 0.886148300 1.123704
#> 858 1.077670 0.886216365 1.123623
#> 859 1.077620 0.886284307 1.123543
#> 860 1.077571 0.886352126 1.123463
#> 861 1.077521 0.886419822 1.123383
#> 862 1.077471 0.886487396 1.123303
#> 863 1.077422 0.886554847 1.123224
#> 864 1.077372 0.886622178 1.123144
#> 865 1.077323 0.886689387 1.123065
#> 866 1.077274 0.886756476 1.122986
#> 867 1.077224 0.886823444 1.122907
#> 868 1.077175 0.886890292 1.122828
#> 869 1.077126 0.886957020 1.122750
#> 870 1.077077 0.887023630 1.122671
#> 871 1.077029 0.887090120 1.122593
#> 872 1.076980 0.887156491 1.122514
#> 873 1.076931 0.887222744 1.122436
#> 874 1.076883 0.887288880 1.122358
#> 875 1.076834 0.887354898 1.122281
#> 876 1.076786 0.887420798 1.122203
#> 877 1.076738 0.887486582 1.122126
#> 878 1.076689 0.887552249 1.122048
#> 879 1.076641 0.887617800 1.121971
#> 880 1.076593 0.887683235 1.121894
#> 881 1.076545 0.887748555 1.121817
#> 882 1.076498 0.887813760 1.121740
#> 883 1.076450 0.887878850 1.121664
#> 884 1.076402 0.887943825 1.121587
#> 885 1.076355 0.888008686 1.121511
#> 886 1.076307 0.888073434 1.121435
#> 887 1.076260 0.888138068 1.121359
#> 888 1.076213 0.888202588 1.121283
#> 889 1.076165 0.888266996 1.121207
#> 890 1.076118 0.888331292 1.121131
#> 891 1.076071 0.888395475 1.121056
#> 892 1.076024 0.888459547 1.120980
#> 893 1.075977 0.888523507 1.120905
#> 894 1.075931 0.888587356 1.120830
#> 895 1.075884 0.888651094 1.120755
#> 896 1.075837 0.888714722 1.120680
#> 897 1.075791 0.888778240 1.120606
#> 898 1.075744 0.888841647 1.120531
#> 899 1.075698 0.888904945 1.120457
#> 900 1.075652 0.888968134 1.120382
#> 901 1.075606 0.889031214 1.120308
#> 902 1.075559 0.889094185 1.120234
#> 903 1.075513 0.889157048 1.120160
#> 904 1.075467 0.889219803 1.120087
#> 905 1.075422 0.889282450 1.120013
#> 906 1.075376 0.889344990 1.119940
#> 907 1.075330 0.889407423 1.119866
#> 908 1.075285 0.889469749 1.119793
#> 909 1.075239 0.889531969 1.119720
#> 910 1.075194 0.889594082 1.119647
#> 911 1.075148 0.889656090 1.119574
#> 912 1.075103 0.889717992 1.119502
#> 913 1.075058 0.889779789 1.119429
#> 914 1.075013 0.889841481 1.119357
#> 915 1.074968 0.889903068 1.119284
#> 916 1.074923 0.889964551 1.119212
#> 917 1.074878 0.890025930 1.119140
#> 918 1.074833 0.890087206 1.119068
#> 919 1.074788 0.890148377 1.118996
#> 920 1.074744 0.890209446 1.118925
#> 921 1.074699 0.890270411 1.118853
#> 922 1.074655 0.890331275 1.118782
#> 923 1.074610 0.890392035 1.118711
#> 924 1.074566 0.890452694 1.118639
#> 925 1.074522 0.890513251 1.118568
#> 926 1.074477 0.890573707 1.118498
#> 927 1.074433 0.890634061 1.118427
#> 928 1.074389 0.890694315 1.118356
#> 929 1.074345 0.890754468 1.118286
#> 930 1.074301 0.890814520 1.118215
#> 931 1.074258 0.890874473 1.118145
#> 932 1.074214 0.890934326 1.118075
#> 933 1.074170 0.890994079 1.118005
#> 934 1.074127 0.891053734 1.117935
#> 935 1.074083 0.891113289 1.117865
#> 936 1.074040 0.891172746 1.117796
#> 937 1.073997 0.891232104 1.117726
#> 938 1.073953 0.891291364 1.117657
#> 939 1.073910 0.891350526 1.117587
#> 940 1.073867 0.891409591 1.117518
#> 941 1.073824 0.891468559 1.117449
#> 942 1.073781 0.891527429 1.117380
#> 943 1.073738 0.891586203 1.117311
#> 944 1.073695 0.891644880 1.117243
#> 945 1.073653 0.891703461 1.117174
#> 946 1.073610 0.891761946 1.117106
#> 947 1.073567 0.891820335 1.117037
#> 948 1.073525 0.891878629 1.116969
#> 949 1.073510 0.891899288 1.116945
#> 950 1.073482 0.891936828 1.116901
#> 951 1.073440 0.891994932 1.116833
#> 952 1.073398 0.892052941 1.116765
#> 953 1.073355 0.892110856 1.116697
#> 954 1.073313 0.892168676 1.116630
#> 955 1.073271 0.892226403 1.116562
#> 956 1.073229 0.892284036 1.116495
#> 957 1.073187 0.892341576 1.116428
#> 958 1.073145 0.892399022 1.116360
#> 959 1.073104 0.892456376 1.116293
#> 960 1.073062 0.892513637 1.116226
#> 961 1.073020 0.892570806 1.116160
#> 962 1.072979 0.892627882 1.116093
#> 963 1.072937 0.892684867 1.116026
#> 964 1.072896 0.892741760 1.115960
#> 965 1.072854 0.892798562 1.115893
#> 966 1.072813 0.892855272 1.115827
#> 967 1.072772 0.892911892 1.115761
#> 968 1.072731 0.892968421 1.115695
#> 969 1.072689 0.893024859 1.115629
#> 970 1.072648 0.893081208 1.115563
#> 971 1.072607 0.893137466 1.115497
#> 972 1.072567 0.893193635 1.115432
#> 973 1.072526 0.893249714 1.115366
#> 974 1.072485 0.893305705 1.115301
#> 975 1.072444 0.893361606 1.115236
#> 976 1.072404 0.893417418 1.115171
#> 977 1.072363 0.893473142 1.115106
#> 978 1.072323 0.893528778 1.115041
#> 979 1.072282 0.893584326 1.114976
#> 980 1.072242 0.893639786 1.114911
#> 981 1.072202 0.893695158 1.114846
#> 982 1.072161 0.893750443 1.114782
#> 983 1.072121 0.893805641 1.114718
#> 984 1.072081 0.893860752 1.114653
#> 985 1.072041 0.893915776 1.114589
#> 986 1.072001 0.893970714 1.114525
#> 987 1.071961 0.894025566 1.114461
#> 988 1.071921 0.894080332 1.114397
#> 989 1.071882 0.894135012 1.114333
#> 990 1.071842 0.894189606 1.114270
#> 991 1.071802 0.894244116 1.114206
#> 992 1.071763 0.894298540 1.114143
#> 993 1.071723 0.894352879 1.114079
#> 994 1.071684 0.894407134 1.114016
#> 995 1.071644 0.894461304 1.113953
#> 996 1.071605 0.894515390 1.113890
#> 997 1.071566 0.894569393 1.113827
#> 998 1.071527 0.894623311 1.113764
#> 999 1.071488 0.894677146 1.113701
#> 1000 1.071449 0.894730898 1.113639
#> 1001 1.071410 0.894784566 1.113576
#> 1002 1.071371 0.894838152 1.113514
#> 1003 1.071332 0.894891655 1.113451
#> 1004 1.071293 0.894945075 1.113389
#> 1005 1.071254 0.894998413 1.113327
#> 1006 1.071216 0.895051670 1.113265
#> 1007 1.071177 0.895104844 1.113203
#> 1008 1.071138 0.895157937 1.113141
#> 1009 1.071100 0.895210948 1.113080
#> 1010 1.071061 0.895263878 1.113018
#> 1011 1.071023 0.895316727 1.112956
#> 1012 1.070985 0.895369496 1.112895
#> 1013 1.070946 0.895422184 1.112834
#> 1014 1.070908 0.895474791 1.112772
#> 1015 1.070870 0.895527319 1.112711
#> 1016 1.070832 0.895579766 1.112650
#> 1017 1.070794 0.895632134 1.112589
#> 1018 1.070756 0.895684422 1.112529
#> 1019 1.070718 0.895736630 1.112468
#> 1020 1.070680 0.895788760 1.112407
#> 1021 1.070643 0.895840811 1.112347
#> 1022 1.070605 0.895892782 1.112286
#> 1023 1.070567 0.895944676 1.112226
#> 1024 1.070530 0.895996491 1.112166
#> 1025 1.070492 0.896048228 1.112105
#> 1026 1.070455 0.896099887 1.112045
#> 1027 1.070417 0.896151468 1.111985
#> 1028 1.070380 0.896202971 1.111925
#> 1029 1.070343 0.896254397 1.111866
#> 1030 1.070306 0.896305746 1.111806
#> 1031 1.070268 0.896357019 1.111746
#> 1032 1.070231 0.896408214 1.111687
#> 1033 1.070194 0.896459332 1.111627
#> 1034 1.070157 0.896510375 1.111568
#> 1035 1.070120 0.896561341 1.111509
#> 1036 1.070083 0.896612231 1.111450
#> 1037 1.070047 0.896663045 1.111391
#> 1038 1.070010 0.896713784 1.111332
#> 1039 1.069973 0.896764447 1.111273
#> 1040 1.069936 0.896815035 1.111214
#> 1041 1.069900 0.896865547 1.111156
#> 1042 1.069863 0.896915985 1.111097
#> 1043 1.069827 0.896966348 1.111038
#> 1044 1.069790 0.897016637 1.110980
#> 1045 1.069754 0.897066851 1.110922
#> 1046 1.069718 0.897116992 1.110864
#> 1047 1.069681 0.897167058 1.110805
#> 1048 1.069645 0.897217050 1.110747
#> 1049 1.069609 0.897266969 1.110689
#> 1050 1.069573 0.897316814 1.110632
#> 1051 1.069537 0.897366586 1.110574
#> 1052 1.069501 0.897416286 1.110516
#> 1053 1.069477 0.897449606 1.110477
#> 1054 1.069465 0.897465912 1.110459
outliers(fp)
#> denominator group numerator rr target_transformed Y
#> 17 120.94 030007 82 0.6780368 0 -0.3885753
#> 28 245.61 030017 131 0.5333603 0 -0.6285476
#> 6 28.80 030025 14 0.4861594 0 -0.7213181
#> 14 73.21 030035 37 0.5054258 0 -0.6824141
#> 32 273.34 030037 145 0.5304793 0 -0.6339827
#> 21 172.38 030043 104 0.6033232 0 -0.5053104
#> 3 19.20 030044 6 0.3125609 0 -1.1631508
#> 4 19.96 030060 7 0.3506260 0 -1.0478201
#> 25 198.94 030062 134 0.6735680 0 -0.3951635
#> 12 45.87 030067 22 0.4796652 0 -0.7347689
#> 2 9.67 030068 2 0.2068827 0 -1.5758811
#> 10 38.92 030073 87 2.2352298 0 0.8043999
#> 7 31.74 030078 55 1.7329455 0 0.5497555
#> 52 685.59 032000 1012 1.4761101 0 0.3894041
#> 22 181.11 032002 283 1.5626043 0 0.4463423
#> 5 24.81 032003 95 3.8296445 0 1.3426301
#> Uzscore rk sp truncated Wuzscore s OD95LCL OD95UCL OD99LCL
#> 17 -4.273269 13 2 0 -4.273269 0.09093164 0.6870374 1.455525 0.5533126
#> 28 -9.850566 2 0 1 NA 0.06380827 0.7024099 1.423670 0.5729580
#> 6 -3.870999 16 2 0 -3.870999 0.18633900 0.6111188 1.636343 0.4600330
#> 14 -5.838929 4 0 1 NA 0.11687316 0.6689770 1.494820 0.5305541
#> 32 -10.481634 1 0 1 NA 0.06048510 0.7039943 1.420466 0.5749970
#> 21 -6.634401 3 0 1 NA 0.07616520 0.6959196 1.436948 0.5646331
#> 3 -5.096671 8 1 0 -5.096671 0.22821773 0.5734589 1.743804 0.4161366
#> 4 -4.681306 12 2 0 -4.681306 0.22383074 0.5774252 1.731826 0.4206837
#> 25 -5.573626 7 1 0 -5.573626 0.07089881 0.6987976 1.431030 0.5683191
#> 12 -4.976398 9 1 0 -4.976398 0.14765074 0.6445616 1.551442 0.5003471
#> 2 -4.900458 10 1 0 -4.900458 0.32157832 0.4908522 2.037273 0.3256333
#> 10 5.018321 50 9 1 NA 0.16029264 0.6338819 1.577581 0.4873387
#> 7 3.097227 48 8 0 3.097227 0.17749926 0.6189345 1.615680 0.4693434
#> 52 10.196068 54 9 1 NA 0.03819159 0.7126729 1.403168 0.5862128
#> 22 6.006746 51 9 1 NA 0.07430684 0.6969535 1.434816 0.5659563
#> 5 6.687592 53 9 1 NA 0.20076436 0.5982289 1.671601 0.4448276
#> OD99UCL LCL95 UCL95 LCL99 UCL99 highlight outlier
#> 17 1.807297 0.8297333 1.194925 0.7423709 1.314130 0 1
#> 28 1.745329 0.8788379 1.133198 0.8143570 1.213308 0 1
#> 6 2.173757 0.6686912 1.437947 0.5211690 1.720387 0 1
#> 14 1.884822 0.7841313 1.256939 0.6773325 1.416488 0 1
#> 32 1.739139 0.8849536 1.125850 0.8234590 1.201382 0 1
#> 21 1.771061 0.8562871 1.160931 0.7810534 1.258467 0 1
#> 3 2.403057 0.6038663 1.558062 0.4393444 1.925512 0 1
#> 4 2.377083 0.6104869 1.545079 0.4474921 1.903227 0 1
#> 25 1.759575 0.8658614 1.149033 0.7951428 1.239064 0 1
#> 12 1.998612 0.7317770 1.334400 0.6049421 1.545676 0 1
#> 2 3.070939 0.4725050 1.857410 0.2885378 2.445625 0 1
#> 10 2.051961 0.7108273 1.367468 0.5766906 1.601235 0 1
#> 7 2.130636 0.6828360 1.413670 0.5396094 1.679236 0 1
#> 52 1.705865 0.9265368 1.077739 0.8861228 1.123734 0 1
#> 22 1.766921 0.8596594 1.156719 0.7860075 1.251593 0 1
#> 5 2.248062 0.6459532 1.478364 0.4919575 1.789136 0 1
source_data(fp)
#> denominator group numerator rr target_transformed Y
#> 46 523.70 030001 406 0.7752585 0 -0.2545658417
#> 48 612.98 030002 642 1.0473450 0 0.0462559947
#> 13 53.79 030003 46 0.8551559 0 -0.1564461798
#> 53 763.72 030006 764 1.0003694 0 0.0003665593
#> 17 120.94 030007 82 0.6780368 0 -0.3885753076
#> 29 250.19 030008 201 0.8034022 0 -0.2189157211
#> 20 155.49 030009 193 1.2412206 0 0.2161087680
#> 45 484.71 030010 569 1.1738860 0 0.1603296602
#> 39 362.22 030011 404 1.1153377 0 0.1091631159
#> 24 188.93 030012 134 0.7092701 0 -0.3435367761
#> 47 554.38 030013 614 1.1075340 0 0.1021445560
#> 49 616.74 030014 491 0.7961241 0 -0.2280034135
#> 38 360.15 030016 501 1.3910974 0 0.3300854897
#> 28 245.61 030017 131 0.5333603 0 -0.6285475889
#> 31 263.56 030018 274 1.0395934 0 0.0388470603
#> 19 154.66 030019 124 0.8017461 0 -0.2209475936
#> 44 475.02 030022 456 0.9599679 0 -0.0408640989
#> 11 38.93 030023 48 1.2328578 0 0.2094358493
#> 42 445.10 030024 429 0.9638358 0 -0.0368420571
#> 6 28.80 030025 14 0.4861594 0 -0.7213180575
#> 37 347.54 030030 369 1.0617593 0 0.0599168777
#> 1 7.56 030033 8 1.0580539 0 0.0565703515
#> 14 73.21 030035 37 0.5054258 0 -0.6824141110
#> 16 118.11 030036 128 1.0837010 0 0.0804138703
#> 32 273.34 030037 145 0.5304793 0 -0.6339826991
#> 43 449.79 030038 493 1.0960592 0 0.0917283669
#> 21 172.38 030043 104 0.6033232 0 -0.5053104431
#> 3 19.20 030044 6 0.3125609 0 -1.1631508098
#> 36 321.86 030055 308 0.9569437 0 -0.0440168854
#> 9 36.56 030059 34 0.9299019 0 -0.0725942220
#> 4 19.96 030060 7 0.3506260 0 -1.0478201218
#> 54 851.72 030061 935 1.0977833 0 0.0932886950
#> 25 198.94 030062 134 0.6735680 0 -0.3951634718
#> 35 302.39 030064 339 1.1210561 0 0.1142825324
#> 40 410.16 030065 458 1.1166280 0 0.1103218566
#> 12 45.87 030067 22 0.4796652 0 -0.7347688553
#> 2 9.67 030068 2 0.2068827 0 -1.5758811289
#> 26 212.34 030069 160 0.7534910 0 -0.2830149484
#> 10 38.92 030073 87 2.2352298 0 0.8043998613
#> 7 31.74 030078 55 1.7329455 0 0.5497554701
#> 34 285.64 030080 252 0.8822420 0 -0.1253031892
#> 23 186.66 030083 174 0.9321958 0 -0.0702334809
#> 8 33.98 030084 43 1.2653820 0 0.2354279994
#> 30 255.65 030085 228 0.8918280 0 -0.1144636926
#> 27 242.03 030086 210 0.8676759 0 -0.1419541547
#> 33 279.48 030087 321 1.1485772 0 0.1385103894
#> 50 619.26 030088 631 1.0189522 0 0.0187806457
#> 51 626.13 030089 543 0.8672318 0 -0.1424486973
#> 18 145.67 030092 105 0.7207832 0 -0.3273834393
#> 41 413.86 030093 389 0.9399266 0 -0.0619484088
#> 15 111.26 030094 92 0.8268712 0 -0.1900812276
#> 52 685.59 032000 1012 1.4761101 0 0.3894040684
#> 22 181.11 032002 283 1.5626043 0 0.4463423162
#> 5 24.81 032003 95 3.8296445 0 1.3426300939
#> Uzscore rk sp truncated Wuzscore s OD95LCL OD95UCL
#> 46 -5.82561011 5 0 1 NA 0.04369771 0.7108599 1.406747
#> 48 1.14522594 37 6 0 1.14522594 0.04039028 0.7119760 1.404542
#> 13 -1.14740235 25 4 0 -1.14740235 0.13634814 0.6538255 1.529460
#> 53 0.01013004 31 5 0 0.01013004 0.03618536 0.7132769 1.401980
#> 17 -4.27326850 13 2 0 -4.27326850 0.09093164 0.6870374 1.455525
#> 29 -3.46267654 18 3 0 -3.46267654 0.06322153 0.7026948 1.423093
#> 20 2.69478189 46 8 0 2.69478189 0.08019527 0.6936106 1.441731
#> 45 3.52983871 49 8 0 3.52983871 0.04542124 0.7102464 1.407962
#> 39 2.07760096 42 7 0 2.07760096 0.05254287 0.7074858 1.413456
#> 24 -4.72197516 11 2 0 -4.72197516 0.07275277 0.6978029 1.433069
#> 47 2.40502171 45 8 0 2.40502171 0.04247137 0.7112832 1.405910
#> 49 -5.66229389 6 1 0 -5.66229389 0.04026697 0.7120161 1.404463
#> 38 6.26423646 52 9 1 NA 0.05269365 0.7074235 1.413580
#> 28 -9.85056605 2 0 1 NA 0.06380827 0.7024099 1.423670
#> 31 0.63066381 34 6 0 0.63066381 0.06159710 0.7034720 1.421521
#> 19 -2.74775672 19 3 0 -2.74775672 0.08041017 0.6934850 1.441992
#> 44 -0.89063114 27 4 0 -0.89063114 0.04588218 0.7100787 1.408295
#> 11 1.30675215 38 6 0 1.30675215 0.16027205 0.6338995 1.577537
#> 42 -0.77727136 29 5 0 -0.77727136 0.04739922 0.7095159 1.409412
#> 6 -3.87099890 16 2 0 -3.87099890 0.18633900 0.6111188 1.636343
#> 37 1.11699588 36 6 0 1.11699588 0.05364109 0.7070285 1.414370
#> 1 0.15554275 32 5 0 0.15554275 0.36369648 0.4558174 2.193861
#> 14 -5.83892910 4 0 1 NA 0.11687316 0.6689770 1.494820
#> 16 0.87392527 35 6 0 0.87392527 0.09201458 0.6863422 1.456999
#> 32 -10.48163426 1 0 1 NA 0.06048510 0.7039943 1.420466
#> 43 1.94539842 40 7 0 1.94539842 0.04715146 0.7096089 1.409227
#> 21 -6.63440091 3 0 1 NA 0.07616520 0.6959196 1.436948
#> 3 -5.09667149 8 1 0 -5.09667149 0.22821773 0.5734589 1.743804
#> 36 -0.78968304 28 5 0 -0.78968304 0.05573994 0.7061314 1.416167
#> 9 -0.43893999 30 5 0 -0.43893999 0.16538530 0.6295011 1.588560
#> 4 -4.68130570 12 2 0 -4.68130570 0.22383074 0.5774252 1.731826
#> 54 2.72255988 47 8 0 2.72255988 0.03426507 0.7138263 1.400901
#> 25 -5.57362633 7 1 0 -5.57362633 0.07089881 0.6987976 1.431030
#> 35 1.98730062 41 7 0 1.98730062 0.05750641 0.7053533 1.417729
#> 40 2.23428317 43 7 0 2.23428317 0.04937685 0.7087574 1.410920
#> 12 -4.97639803 9 1 0 -4.97639803 0.14765074 0.6445616 1.551442
#> 2 -4.90045823 10 1 0 -4.90045823 0.32157832 0.4908522 2.037273
#> 26 -4.12406291 14 2 0 -4.12406291 0.06862527 0.6999894 1.428593
#> 10 5.01832060 50 9 1 NA 0.16029264 0.6338819 1.577581
#> 7 3.09722689 48 8 0 3.09722689 0.17749926 0.6189345 1.615680
#> 34 -2.11773511 21 3 0 -2.11773511 0.05916849 0.7046022 1.419241
#> 23 -0.95955489 26 4 0 -0.95955489 0.07319381 0.6975633 1.433562
#> 8 1.37236552 39 7 0 1.37236552 0.17154905 0.6241482 1.602184
#> 30 -1.83016671 23 4 0 -1.83016671 0.06254277 0.7030216 1.422431
#> 27 -2.20842527 20 3 0 -2.20842527 0.06427845 0.7021800 1.424136
#> 33 2.31556895 44 8 0 2.31556895 0.05981700 0.7043042 1.419841
#> 50 0.46735515 33 6 0 0.46735515 0.04018495 0.7120426 1.404410
#> 51 -3.56443532 17 3 0 -3.56443532 0.03996389 0.7121140 1.404270
#> 18 -3.95131604 15 2 0 -3.95131604 0.08285428 0.6920385 1.445006
#> 41 -1.26025051 24 4 0 -1.26025051 0.04915563 0.7088437 1.410748
#> 15 -2.00497405 22 4 0 -2.00497405 0.09480483 0.6845252 1.460867
#> 52 10.19606797 54 9 1 NA 0.03819159 0.7126729 1.403168
#> 22 6.00674614 51 9 1 NA 0.07430684 0.6969535 1.434816
#> 5 6.68759184 53 9 1 NA 0.20076436 0.5982289 1.671601
#> OD99LCL OD99UCL LCL95 UCL95 LCL99 UCL99 highlight outlier
#> 46 0.5838633 1.712730 0.9161767 1.089431 0.8703859 1.142533 0 0
#> 48 0.5853093 1.708499 0.9223928 1.082393 0.8798183 1.131211 0 0
#> 13 0.5117322 1.954147 0.7507815 1.305456 0.6309291 1.497241 0 0
#> 53 0.5869963 1.703588 0.9303262 1.073510 0.8918993 1.116945 0 0
#> 17 0.5533126 1.807297 0.8297333 1.194925 0.7423709 1.314130 0 1
#> 29 0.5733244 1.744213 0.8799161 1.131898 0.8159596 1.211196 0 0
#> 20 0.5616822 1.780366 0.8489973 1.170116 0.7703759 1.273474 0 0
#> 45 0.5830690 1.715063 0.9129459 1.093117 0.8654950 1.148468 0 0
#> 39 0.5794998 1.725626 0.8996571 1.108474 0.8454632 1.173251 0 0
#> 24 0.5670442 1.763531 0.8624847 1.153208 0.7901652 1.245868 0 0
#> 47 0.5844115 1.711123 0.9184791 1.086816 0.8738761 1.138325 0 0
#> 49 0.5853612 1.708347 0.9226250 1.082132 0.8801712 1.130791 0 0
#> 38 0.5794194 1.725866 0.8993768 1.108802 0.8450421 1.173780 0 0
#> 28 0.5729580 1.745329 0.8788379 1.133198 0.8143570 1.213308 0 1
#> 31 0.5743246 1.741176 0.8829048 1.128304 0.8204064 1.205363 0 0
#> 19 0.5615218 1.780875 0.8486095 1.170608 0.7698091 1.274278 0 0
#> 44 0.5828519 1.715702 0.9120828 1.094104 0.8641899 1.150060 0 0
#> 11 0.4873600 2.051871 0.7108611 1.367413 0.5767359 1.601144 0 0
#> 42 0.5821237 1.717848 0.9092451 1.097361 0.8599027 1.155310 0 0
#> 6 0.4600330 2.173757 0.6686912 1.437947 0.5211690 1.720387 0 1
#> 37 0.5789093 1.727386 0.8976167 1.110861 0.8423994 1.177110 0 0
#> 1 0.2897498 3.451253 0.4192450 2.007393 0.2339215 2.709899 0 0
#> 14 0.5305541 1.884822 0.7841313 1.256939 0.6773325 1.416488 0 1
#> 16 0.5524300 1.810184 0.8278028 1.197455 0.7395815 1.318286 0 0
#> 32 0.5749970 1.739139 0.8849536 1.125850 0.8234590 1.201382 0 1
#> 43 0.5822441 1.717493 0.9097083 1.096829 0.8606020 1.154451 0 0
#> 21 0.5646331 1.771061 0.8562871 1.160931 0.7810534 1.258467 0 1
#> 3 0.4161366 2.403057 0.6038663 1.558062 0.4393444 1.925512 0 1
#> 36 0.5777516 1.730848 0.8937236 1.115437 0.8365630 1.184512 0 0
#> 9 0.4820390 2.074521 0.7024797 1.380998 0.5655515 1.624034 0 0
#> 4 0.4206837 2.377083 0.6104869 1.545079 0.4474921 1.903227 0 1
#> 54 0.5877093 1.701521 0.9339606 1.069477 0.8974496 1.110477 0 0
#> 25 0.5683191 1.759575 0.8658614 1.149033 0.7951428 1.239064 0 1
#> 35 0.5767482 1.733859 0.8904537 1.119303 0.8316701 1.190770 0 0
#> 40 0.5811429 1.720747 0.9055527 1.101621 0.8543334 1.162182 0 0
#> 12 0.5003471 1.998612 0.7317770 1.334400 0.6049421 1.545676 0 1
#> 2 0.3256333 3.070939 0.4725050 1.857410 0.2885378 2.445625 0 1
#> 26 0.5698481 1.754854 0.8700115 1.143932 0.8012731 1.230759 0 0
#> 10 0.4873387 2.051961 0.7108273 1.367468 0.5766906 1.601235 0 1
#> 7 0.4693434 2.130636 0.6828360 1.413670 0.5396094 1.679236 0 1
#> 34 0.5757801 1.736774 0.8873825 1.122951 0.8270823 1.196683 0 0
#> 23 0.5667372 1.764486 0.8616824 1.154203 0.7889839 1.247490 0 0
#> 8 0.4755921 2.102642 0.6924472 1.397536 0.5522544 1.651950 0 0
#> 30 0.5737449 1.742935 0.8811643 1.130395 0.8178159 1.208756 0 0
#> 27 0.5726624 1.746230 0.8779744 1.134242 0.8130742 1.215003 0 0
#> 33 0.5753962 1.737933 0.8861857 1.124378 0.8252964 1.198996 0 0
#> 50 0.5853956 1.708247 0.9227794 1.081958 0.8804059 1.130511 0 0
#> 51 0.5854881 1.707977 0.9231957 1.081489 0.8810388 1.129758 0 0
#> 18 0.5596763 1.786747 0.8442051 1.176214 0.7633805 1.283451 0 0
#> 41 0.5812543 1.720417 0.9059653 1.101144 0.8549553 1.161412 0 0
#> 15 0.5501260 1.817765 0.8228397 1.203997 0.7324247 1.329040 0 0
#> 52 0.5862128 1.705865 0.9265368 1.077739 0.8861228 1.123734 0 1
#> 22 0.5659563 1.766921 0.8596594 1.156719 0.7860075 1.251593 0 1
#> 5 0.4448276 2.248062 0.6459532 1.478364 0.4919575 1.789136 0 1
phi(fp)
#> [1] 8.532851
tau2(fp)
#> [1] 0.02841023